а). (59°; 59°; 62) или (56°; 62°; 62°) ;
б). (41°; 41°; 98°) .
а). Один из углов равен 62°.
В равнобедренном треугольнике по крайней мере два равных угла. Сумма всех углов - 180°. Если угол в 62° - "единственный в своем роде", то каждый из двух других равных углов будет равен:
(180° - 62°) : 2 = 118° : 2 = 59°.
Если же существуют два таких угла, то оставшийся угол равен:
180° - 62° * 2 = 180° - 124° = 56° градусов.
Оба исхода имеют место быть.
Углы искомого треугольника: (59°; 59°; 62) или (56°; 62°; 62°).
б). Один из углов равен 98°.
В равнобедренном треугольнике не может быть два угла по 98°, так как 98° * 2 = 196° > 180°.
Если угол в 98° единственен, то каждый из оставшихся углов равен:
(180° - 98°) : 2 = 82° : 2 = 41°.
Углы искомого треугольника: (41°; 41°; 98°).
Задача решена!
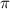×D=5×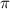. Отсюда D=5. Из чертежа видно, что так как окружности касаются, то средняя линия трапеции равна диаметру D. Площадь трапеции равна произведению полусуммы оснований, то есть средней линии, на высоту. Высоту определяем из треугольника, где одна сторона - боковая сторона трапеции (она же гипотенуза) = 5, вторая сторона - высота трапеции, опущенная из верхней точки боковой стороны - х, третья сторона - отрезок нижнего основания трапеции от нижней точки боковой стороны до высоты =3 по условию задачи. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. 5²=3²+х². х=√25-9=√16=4. Площадь трапеции S=5×4=20
12
Объяснение:
Диагональ прямоугольника образует два равных прямоугольных треугольников является гипотенузой. Угол, который образуется шириной(катетом) и диагональю(гипотенузой) равен 60°. Значит другой острый угол равен 30°. Катет лежащий против угла 30° равен половине гипотенузе. Ширина прямоугольника и является катетом, который лежит против угла 30°.
Катет(ширина)=8√3/2=4√3.
ДЛина прямоугольника будет являться катетом прямоугольного треугольника. Мы можем его найти по теореме Пифагора.
Катет(ширина) обозначим а, гипотенуза(диагональ) обозначим с, катет(длина) обозначим б.
Найдём его по теореме Пифагора:
б^2=с^2-а^2
б^2=(8√3)^2-(4√3)^2=192-48=144
б=√144=12
Длина больше ширины а прямоугольнике. Если корень в квадрате, то корень убирается.