В условии опечатка: в пункте б) надо найти отношение площадей треугольника ВОС и НЕвыпуклого пятиугольника AOBCD.
а) ∠ОВС = ∠ОСВ по условию, значит ΔОВС равнобедренный с основанием ВС, ОВ = ОС.
АС = CD по условию, значит ΔACD равнобедренный с основанием AD, ∠CAD = ∠CDA.
О - середина АС, значит
ОВ = ОС = ОА.
Итак, AD = 2BC (по условию), AC = 2OC и CD = 2OB, тогда
ΔADC подобен ΔСОВ по трем пропорциональным сторонам. Значит
∠ВСО = ∠DAC, а эти углы накрест лежащие при пересечении прямых AD и ВС секущей АС, значит BC║AD.
б) Коэффициент подобия треугольников ВОС и DAC:
k = 1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sboc : Sdac = k² = 1/4
Т.е. Sdac = 4Sboc, тогда площадь пятиугольника AOBCD:
Saobcd = Sboc + Sdac = 5Sboc,
Sboc : Saobcd = 1 : 5
18
Объяснение:
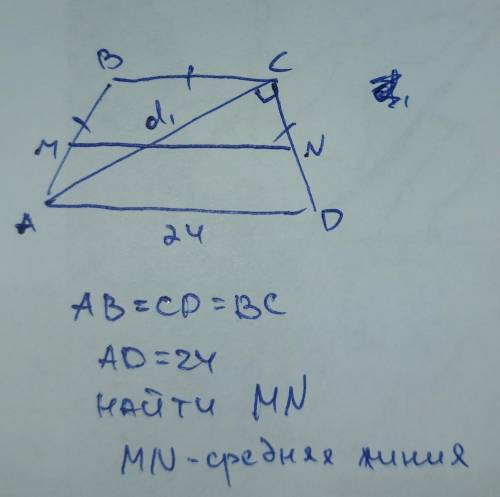
Пусть АС = х, АВ = ВС = СD = у.
Так как сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение оснований трапеции, то для данной равнобедренной трапеции:
2х² = 2у²+ 2у ·24
или
х² - у² - 24у= 0 (1)
Так как:
х² = 24² - у²,
то перепишем (1) в виде:
24² - у² - у² - 24у = 0
-2у² - 24у + 576 = 0
у² + 12у - 288 = 0
у₁,₂ = - 6 ±√(36+288) = -6±√324 = -6±18
у = -6+18 = 12
Средняя линия:
(24 + 12) : 2 = 36 : 2 = 18
ответ: 18