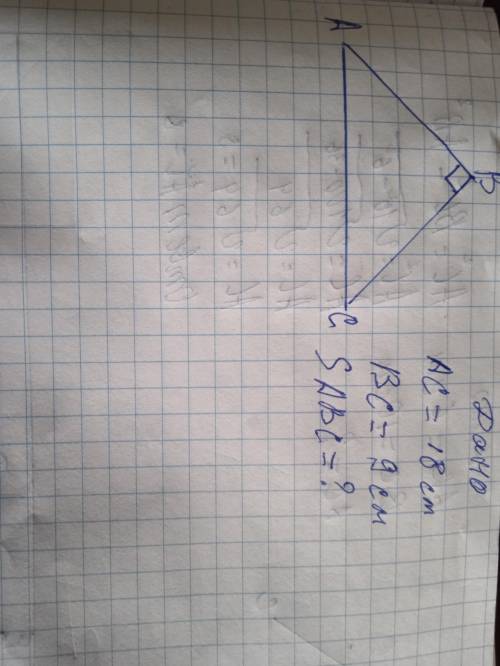
≈ 70,15 см²
Объяснение:
Катет ВС равен половине гипотенузы АС, значит ∠А=30°,
тогда ∠С=90-30=60°
S=1/2 * АС * ВС * sin60° = 1/2 * 18 * 9 * √3/2 = 81√3/2 ≈ 70,15 см²
1) Вписанные углы - угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.
2) Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°.
3) Угол с вершиной в центре окружности называется центральным углом.
4) Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
5) 180°
6) Внешние углы - это углы, смежные с углами треугольника.
7) Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
8) S=1/2 a*hª-треугольник. Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
9)
81√3 / 2 см²
Объяснение:
1) ΔABC — прямоугольный (∠B = 90°), тогда по теореме Пифагора
AB²+BC² = AC², отсюда AB = √(AC²-BC²)
AB = √(18²-9²) = √(18-9)(18+9) = √(9*27) = √3⁵ = 9√3 (см)
2) Площадь прямоугольного треугольника равна половине произведения катетов:
S = (AB×BC)/2 = (9√3 × 9)/2 = 81√3 / 2 (см²)