Question

В равнобедренный треугольник ABC с основанием AC вписана окружность. Она касается стороны BC в точке P. Отрезок AP пересекает окружность точке D. Найдите площадь треугольника ABC, если известно, что AC = $4 \sqrt{2}$
, DP = 2. ​

Answer 1

$AK=KC=4\sqrt{2}/2=2\sqrt{2}$, так как точка K является серединой отрезка АС. Тогда $KC=PC=2\sqrt2$ как касательные окружности.

По теореме о секущей и касательной: $AP\cdot AD=AK^2$

$(2\sqrt2)^2=AD\cdot(2+AD)$

$8=2AD+AD^2$

$AD^2+2AD-8=0$

По теореме Виета, получим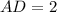 $AD=2$.

Рассмотрим треугольник APC со сторонами AP = 4; PC =2√2 и AC = 4√2 и пусть ∠C = α. Используем теорему косинусов:

cos α = (a² + b² - c²)/2ab = ((4√2)² + (2√2)² - 4²)/[2*4√2*2√2] = 3/4

Из определения косинуса cos a = CK / BC отсюда BC = CK/cosa тогда получим BC = 2√2 / [3/4] = 8√2/3

По теореме Пифагора:

$BK^2=BC^2-CK^2=\dfrac{128}{9}-8=\dfrac{56}{9}$

$BK=\dfrac{2\sqrt{14}}{3}$

Искомая площадь треугольника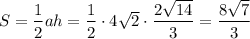 $S=\dfrac{1}{2}ah=\dfrac{1}{2}\cdot4\sqrt{2}\cdot\dfrac{2\sqrt{14}}{3}=\dfrac{8\sqrt{7}}{3}$ кв. ед.