неизвестная длина=5
Объяснение:
Начнём с верхнего квадрата с площадью 17(ед²) - найдём вторую его сторону: 17÷5=3,4 - вторая сторона фигуры. Общая длина стороны фигур с площадью 60 и 17 составляет 9, тогда длина фигуры площадью 60(ед²) равна: 9–3,4=5,6. Сложим площади 60 + 52=112(ед²) - общая площадь площадей 60 и 52. У фигуры с этой площадью ширина 5,6, которую мы нашли, тогда длина этого прямоугольника=112÷5,6=20. Эта длина является самой большой, включая в себя длину 5 и 10. Теперь найдём неизвестную длину:
20–5–10=5
52 см.
Объяснение
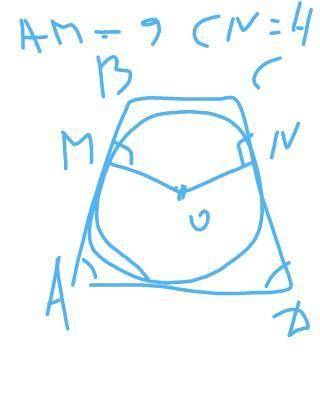
1. Углы трапеции равны, следовательно, трапеция - равнобедренная → AB = CD, BM = CN и AM = DN
2. Вспомним свойство трапеции: В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
В трапецию вписана окружность, следовательно, сумма длин оснований AD и BC равна сумме длин боковых сторон AB и CN.
AD + BC = AB + CD
AB = AM + MB = 9 + 4 = 13 см
CD = DN + CN = 9 + 4 = 13 см
отсюда AD + BC = 13 + 13 = 26 см
3. Периметр трапеции - сумма длин её сторон.
P = AD + BC + AB + CD = (AD + BC) + AB + CD = 26 + 13 + 13 = 52 см