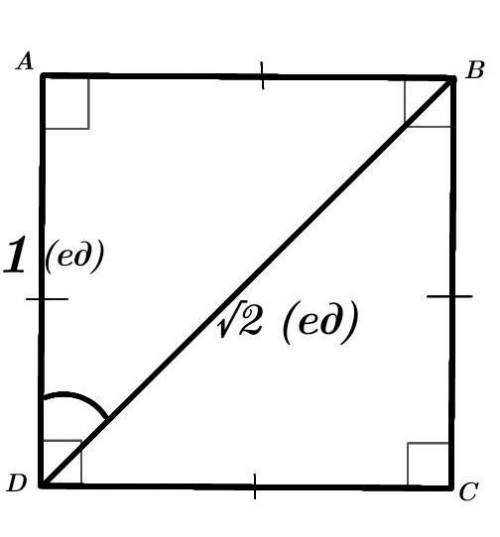
Дано :
Четырёхугольник ABCD — квадрат.
AD = 1 (ед).
BD — диагональ = √2 (ед).
Найти :
соs(∠BDA) = ?
Квадрат — четырёхугольник, всё стороны которого равны, а все углы прямые.
Рассмотрим прямоугольный ∆ABD.
Косинус острого угла прямоугольного треугольника — отношение прилежащего катета к гипотенузе.
В нашем случае катет, прилежащий к ∠BDA — AD, а гипотенуза — BD (так как лежит против прямого угла).
То есть —
cos(∠BDA) = AD/BD
cos(∠BDA) = 1 (ед) / √2 (ед)
cos(∠BDA) = 1/√2
Или —
cos(∠BDA) = (√2)/2 (одно и тоже).
(√2)/2.
ответ: довжина другої діагоналі дорівнює 9 .
Объяснение:
ABCD - трапеція , АС = 3√6 ; ∠CAD = 60° , ∠BDA = 45° ; BD -?
Опустимо перпендикуляри BN i CM на основу AD трапеції ; BN = CM .
Із прямокутного ΔАСМ СМ = АСsin60° = 3√6 * √3/2 = 9√2/2 ;
із прямокутного ΔBND BD = BN/sin45° = ( 9√2/2 ) : ( √2/2 ) = 9 .