Question

Вычислите неизвестную площадь по рисунку.

Answer 1

Вычислите неизвестную площадь по рисунку.

Объяснение:

1) S( желтого )=S( зеленого) т.к высота из вершины одна и та же, основания равны.

2) Соединим тоску О с вершинами 4-х угольника .Т.к по условию М, Р,Н,Т- середины сторон , то

S(ВМ)=S(МС) ( в скобках указано основание треугольника),

S(СР)=S(РК) ,

S(КН)=S(АН) ,

S(АТ)=S(ТВ) , рисунок г1.

3) По рисунку г2 , S1+S3  состоит из  площадей треугольников а ,в, f, c . А ,  сумма площадей х+S2 состоит  из площадей треугольников а ,в, f, c ⇒  S1+S3  = х+S2 ⇒

х=S1+S3- S2.

Answer 2

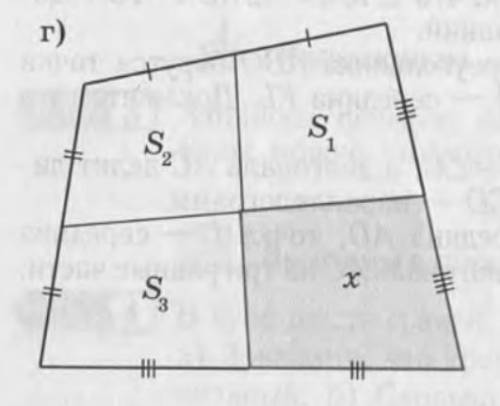
x = S1 +S3 - S2

Объяснение:

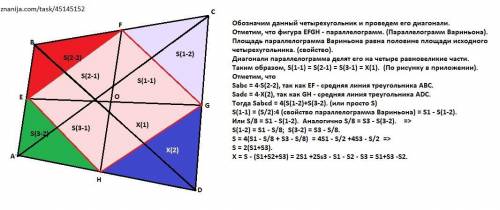
Обозначим данный четырехугольник и проведем его диагонали.

Отметим, что фигура EFGH - параллелограмм. (Параллелограмм Вариньона). Площадь параллелограмма Вариньона равна половине площади исходного четырехугольника. (свойство).

Диагонали параллелограмма делят его на четыре равновеликие части.

Таким образом, S(1-1) = S(2-1) = S(3-1) = X(1).  (По рисунку в приложении).

Отметим, что

Sabc = 4·S(2-2), так как EF - средняя линия треугольника АВС.

Sadc = 4·X(2), так как GH - средняя линия треугольника ADC.

Тогда Sabcd (или просто S) = 4(S(1-2)+S(3-2).

S(1-1) = (S/2):4 (свойство параллелограмма Вариньона) = S1 - S(1-2).

Или S/8 = S1 - S(1-2).  Аналогично S/8 = S3 - S(3-2).    =>

S(1-2) = S1 - S/8;  S(3-2) = S3 - S/8.

S = 4(S1 - S/8 + S3 - S/8)  = 4S1 - S/2 +4S3 - S/2  =>

S = 2(S1+S3).

X = S - (S1+S2+S3) = 2S1 +2S3 - S1 - S2 - S3 = S1+S3 -S2.