ответ: 20 см
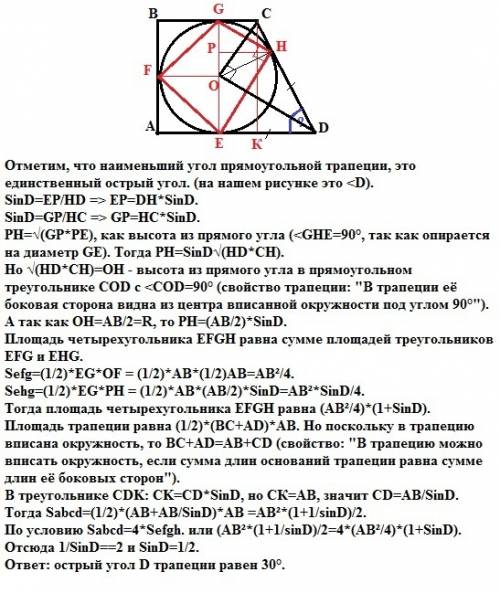
Решение: смотри рисунок.
Пусть треугольник BAC равнобедренный, AB=AC=10 см.
Возьмем произвольную точку K на основании BC и проведем KM||AC иKN||AB
KM=AN, KN=AM -противоположные стороны параллелограмма.
Докажем, что KM=BM. Угол 2=углу 4 как соответственные углы при AC||KM и секущей KC. Но угол 4=углу 1 (углы при основании равнобедренного треугольника). Отсюда угол 2=углу 1. Значит треугольник BMK равнобедренный и KM=BM как его боковые стороны.
Аналогично докажем, что KN=NC. Угол 3=углу 1 как соответственные углы при AB||KN и секущей KB. Но угол 1=углу 4 (углы при основании равнобедренного треугольника). Отсюда угол3 =углу 4. Значит треугольник KNC равнобедренный и KN=NC как его боковые стороны.
Периметр параллелограмма =KM+MA+AN+NK=BM+MA+AN+NC=BA+AC=10+10=20 (см)
∠АМС = 30°
Объяснение:
Дано:
Треугольник АВС: ВС = АВ
ВМ = АС
∠АВС = 20°
Найти:
∠АМС
Cмотри прикреплённый рисунок
Сделаем дополнительные построения:
1) Cтроим параллелограмм АВТС. По свойству параллелограмма диагональ ВС делит его на два равных треугольника: ΔТСВ = ΔАВС
2) Приняв ВС за ось симметрии, построим ΔСВК симметричный ΔСВТ.
ΔСВТ = ΔСВК по построению.
При этом ∠СВК = 0,5 · (180° - 20°) =80°, ∠АВС = 20°, тогда
∠КВМ = 80° - 20° = 60°.
По условию ВМ = АС, а АС = ВТ и ВТ = ВК по построению. Тогда ВМ = ВК и ΔМВК равнобедренный. Поскольку угол при вершине В треугольника МВК равен 60°, то два угла при основании ВК равны по 60°, и ΔМВК - равносторонний.
Проекции НВ и НК сторон МВ и МК в Δ МВК являются и проекциями сторон СВ и СК равнобедренного ΔСВК. то точки Н, М и С лежат на общем перпендикуляре СН, являющимся высотой, медианой и биссектрисой обоих равнобедренных треугольников: ΔМВК и ΔСВК.
Поскольку МН - биссектриса угла КМВ. то ∠ВМН = ∠КМН = 30°.
∠АМС и ∠ВМН - вертикальные углы. поэтому ∠АМС = 30°