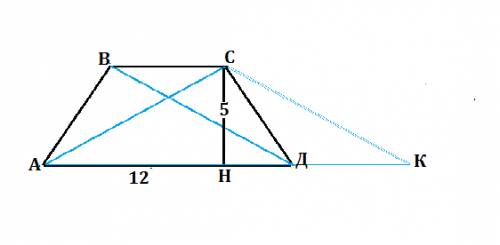
1) Рассмотрим сечение, проходящее через центры сфер.
Отрезок, соединяющий центры, перпендикулярен диаметру сечения. Точкой пересечения они делятся пополам и образуют прямоугольный треугольник с катетами 5 и 12. Гипотенуза этого треугольника - искомый радиус. Треугольник с катетами 5 и 12 из Пифагоровых троек (прямоугольные треугольники с целочисленными сторонами), следовательно, R=13 (можно решить по т.Пифагора с тем же результатом).
* * *
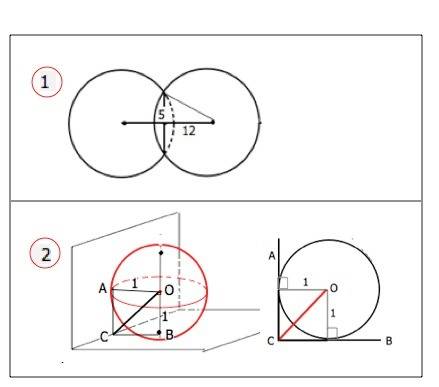
2) Центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости, т.е. на плоскости, делящей этот двугранный угол пополам.
Искомое расстояние - диагональ квадрата со сторонами, равными радиусу шара ( биссектриса СО его прямого угла - см. рисунок),
СО=r:sin45°=√2
35°
Объяснение:
Сумма углов 290°, дана сумма вертикальных углов.
<1+<3=290°
Полный угол 360°
<2+<4=360°-290°=70°
<2=<4, вертикальные углы
<2=70°/2=35°