см объяснение
Объяснение:
1) ∠4 = ∠3= 120° как соответственные углы,
2) см. фото. Пусть ∠1 = 62°.
∠3 = ∠1 = 62° как вертикальные углы,
∠5 = ∠1 = 62° как соответственные углы,
∠7 = ∠5 = 62° как вертикальные углы,
∠2 = 180° - ∠1 по свойству смежных углов, 180° - 62° =118°
∠4 = ∠2 = 118° как вертикальные,
∠6 = ∠2 = 118° как соответственные,
∠8 = ∠6 = 118° как вертикальные.
3) Углы при параллельных прямых и секущей-
Накрест лежащие углы равны, то есть, если их сумма равна 110°, то каждый из них равен 55° (110:2=55)
Найдем смежный угол. Сумма смежных углов равна 180°.
180-55=125°
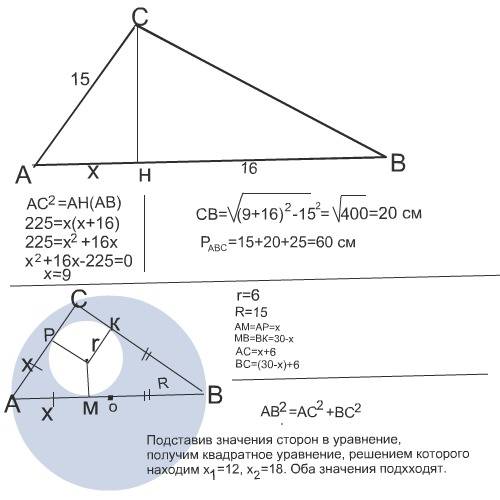
1)Пусть ABC — данный треугольник (угол C — прямой, AC = 15); CD — высота; BD = 16. Обозначим BD = x. Из подобия треугольников ABC и ACD (угол A общий, ⁄ ADC = ⁄ ACB = 90°) получаем
2)
Пусть а и в катеты треугольника, тогда с=30, т.к. радиус описанной окружности равен половине гипотенузы r=p-c,p=r+c=36, P=36*2=72,a+b=72-30=42.имеем
{а+в=42
a^2+b^2=900
{a^2+b^2=2*ab=42^2=1764
a^2+b^2=900
{900+2*ab=1764
2ab=1764-900
{a+b=42
ab=432
a^2-42a+432=0
а1=18,а2=24
в1=24, в2=18
Строим сечение.
Соединяешь К и Р, поскольку они лежат в одной плоскости. (Кстати, как не располагай эти три точки, то две из них всегда будут лежать в одной плоскости)
КР - одна сторона сечения.
ОК - линия пересечения плоскостей АОС и ВОС. На этой прямой будет лежать общая точка, по которой плоскость сечения пересечет эти две плоскости. Поэтому продлеваешь кант ОС и проводишь прямую КТ, поскольку точки К и Т лежат в одной плоскости. Прямая КТ пересечет ОК в точке Е. Точки Е и Р лежат в одной плоскости ВОС, поэтому проводишь прямую ЕР. Она пересечет плоскость АВС в точке М. Точки М и Т лежат в одной плоскости АВС, поэтому соединяешь М и Т.
ТКРМ - искомое сечение.
(Кстати, чертить проще чем объяснять)