Из точки А проведены две секущие АВ и АС, которые пересекают окружность в точках К и М так, что AB = 2 см, ВС = 4 см, AC = 5 см, AK = 1 см. Найдите МК.
Объяснение:
1)∠AKM =180°-∠BKM по т. о смежных углах ; ∠C=180°-∠BKM по свойству углов вписанного 4-х угольника ⇒ ∠AKM =∠C.
2) ΔAKM ~ΔACB по двум углам : ∠A_общий , ∠AKM =∠C.
Сходственные стороны в подобных треугольниках пропорциональны : , ⇒ MK=(1*4):5=0,8 (см)
============================
Свойство углов вписанного 4-х угольника
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Рисунок вам нарисовала. Там все ясно-понятно. Треугольник FAB равносторонний. Все стороны равны, все углы по 60, такой вывод делаем из условия. Сторону этого треугольника обозначаем х. Δ FMA: М = 90 FM - бисектриса, медиана, высота FM = хsina = x√3/2 Чтобы найти угол между мимобегущими, нужно найти угол между паралельными им прямыми, которые пересекаются. Перенесем AC в ML, это будет средняя линия треугольника ABC Чтобы узнать AC найдем диагональ квадрата d² = 2a² Сторона у нас х d² = 2x² d = x√2 ML = x√2/2 ΔFMO₁ (O₁ = 90) MO₁ = x√2/4 MO₁/FM = cos a = x√2/4/x√3/2 = √2/2√3 = √6/6 Не знаю, почему значение не табличное, может я ошиблась, но вроде все правильно было :)
Из точки А проведены две секущие АВ и АС, которые пересекают окружность в точках К и М так, что AB = 2 см, ВС = 4 см, AC = 5 см, AK = 1 см. Найдите МК.
Объяснение:
1)∠AKM =180°-∠BKM по т. о смежных углах ; ∠C=180°-∠BKM по свойству углов вписанного 4-х угольника ⇒ ∠AKM =∠C.
2) ΔAKM ~ΔACB по двум углам : ∠A_общий , ∠AKM =∠C.
Сходственные стороны в подобных треугольниках пропорциональны :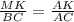 ,
,  ⇒ MK=(1*4):5=0,8 (см)
⇒ MK=(1*4):5=0,8 (см)
============================
Свойство углов вписанного 4-х угольника
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.