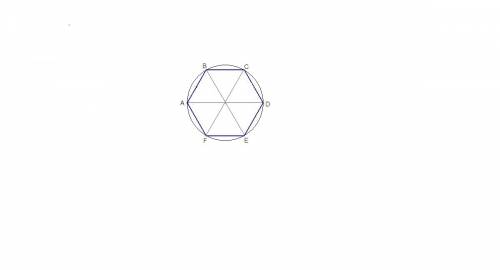
1) В правильном шестиугольнике все стороны равны.
P₆ = 6a₆,
где а₆ - сторона шестиугольника.
6а₆ = 48
а₆ = 8 м
Радиус окружности, описанной около правильного шестиугольника, равен его стороне:
R = a₆ = 6 м
Эта же окружность описана около квадрата.
Радиус окружности, описанной около квадрата:
R = a₄√2 / 2
6 = a₄ √2 / 2
a₄ = 12 / √2 = 6√2 м
2) Шестиугольник диагоналями делится на 6 равных равносторонних треугольников, так как центральный угол его равен 360°/6 = 60°.
Площадь одного треугольника:
S = a²√3/4 = 72√3 / 6
a²√3/4 = 12√3
a² = 48
a = 4√3 см - сторона шестиугольника.
Радиус окружности, описанной около правильного шестиугольника, равен его стороне:
R = a = 4√3 см
Длина окружности:
C = 2πR = 2π · 4√3 = 8π√3 см
ΔАВС прямоугольный, <C=90, т.О - центр впис. окружности, ОМ перпендикулярно
АВ, ОН перп-но СВ, ОК перп-но АС, ОМ=ОН=ОК=r -радиус вписан. окр.
АМ=9,ВМ=6
АМ=АК=9, ВМ=ВН=6 (как отрезки касательных, проведённых из одной точки к окр-ти). ---> АВ=9+6=15, АС=9+r, DC=6+r
По теореме Пифагора: АС²+ВС²=АВ²
(6+r)²+(9+r)²=15² ---> r²+15²-54=0 ---> r=-18<0 (не подходит), r=3>0.
S=pr , p - полупериметр
р=0,5(АВ+АС+ВС)=0,5((9+3)+(6+3)+15)=0,5*36=18 S=18*3=54