угол АОВ= 180°
угол COB=43°
PO- биссектр. угла AOC
найти угол АОР
180-43=137°(УГОЛ АОС)
137:2=68,5°( УГОЛ АОР )
( СОВЕТУЮ ПРОВЕРИТЬ ДАНО В ЗАДАЧИ , ПОТОМ КАК ОТВЕД НЕ МОЖЕТ БЫТЬ В ДЕСЯТИЧНОЙ ДРОБИ. ЕСЛИ ЖЕ В КНИГЕ ДАНО ИМЕННО ТАКОЕ , ЗНАЧИТ ЭТО ОПЕЧАТКА)
рассмотрим треугольник абе, параллелограмм абсд. так как сумма углов треугольника равна 180 градусов то угол абе равен 180-90(угол аеб)-60(угол бае) =30 градусов. в прямоугольном треугольнике катет напротив угла в 30 градусов равен половине гипотенузы, значит 2ае=ба, отсюдого следует что 2ае=ад - ад=ба. так как в параллелограмме противоположные стороны попарно равны, то ад=вс=ба=сд. значит все стороны этого параллелограмма равны, значит каждая сторона этого параллелограмма равна 36/4=9
теперь рассмотрим треугольник бсд. так как бс=сд, трегольник является равнобедренным или равносторонним. значит углы у основания бд равны.Также по свойству параллелограмма противоположные углы попарно равны, то есть угол бад равен углу бсд. сумма углов треугольника равна 180 градусов, значит угол сбд или сдб равны (180-60)/2=60 градусов. так как в этом треугольнике все углы равны 60 градусов треугольник - равносторонний, значит бд=вс=сд=9
ответ бд равен 9
Объяснение:
∠С=30°,∠А=90°,∠В=60°
Объяснение:
Дано: AD⊥BC, ВО=ОС. ∠ВАD=∠DАО=∠ОАС
Найти: ∠А,∠В,∠С ΔАВС
Пусть ∠ВАD=∠DАО=∠ОАС=х
1) Рассмотрим ΔВАО. АD - высота. ∠ВАD=∠DАО ⇒ АD - биссектриса.
Если в треугольнике медиана совпадает с биссектрисой, то треугольник равнобедренный. ⇒ΔВАО - равнобедренный. В равнобедренном треугольнике высота является также медианой. ⇒
ВD=DО=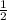 
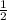ВО= ОС.
2) Дополнительное построение: Проведём ОМ⊥АС.
Рассмотрим прямоугольные треугольники АDО и АМО.
∠DАО=∠ОАС - по условию, АО - общая.
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.⇒ΔАDО = ΔАМО
Из равенства треугольников следует равенство катетов:
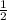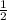DО = МО = ВО= ОС.
3) Рассмотрим прямоугольный треугольник ОМС (∠М=90°).
Из доказанного выше МО=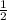ОС. Т.е. катет МО равен половине гипотенузы ОС.
Следовательно ∠С=30°
4) Рассмотрим прямоугольный треугольник АDC(∠D=90°).
По свойству острых углов прямоугольного треугольника
∠DАС=90°-∠С=90°-30°=60°.
По условию ∠DАС=2х ⇒ 2х=60°, х=30°
5) ∠ВАС=3х=3*30°=90°
∠А треугольника АВС = 90°
Так как сумма углов треугольника равна 180°, то ∠В треугольника АВС будет равен: ∠В=180°-∠А-∠С=180°-90°-30°=60°
