Впрямоугольном треугольнике к гипотенузе ас проведенна высота вд.вс=2 см,ад=3 см.найти: дс,вд,ав

👇

Ответ:

5286Squirrel17

17.03.2020

Смотри фото решение на листе
Впрямоугольном треугольнике к гипотенузе ас проведенна высота вд.вс=2 см,ад=3 см.найти: дс,вд,ав

4,8(69 оценок)

Открыть все ответы

Ответ:

Milanusia

17.03.2020

Сделаем рисунок.
а) В ∆ АВС отрезок EF соединяет середины сторон АВ и АС⇒
EF– средняя линия.⇒

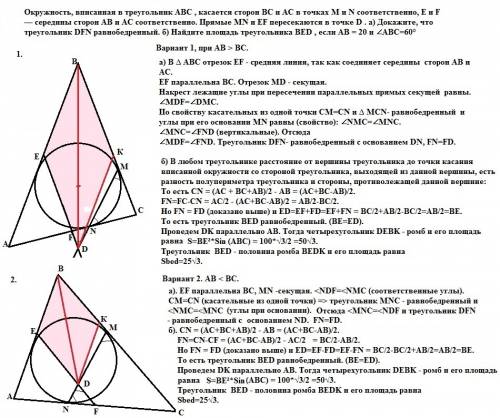
ЕF и ВС параллельны. Отрезок MN - секущая при них.

Соответственные углы при пересечении параллельных прямых секущей равны. ∠NDF=∠NMC

По свойству касательных из одной точки СМ=CN и ∆ МСN- равнобедренный. ⇒ углы при его основании MN равны ( свойство).

∠NDF=∠NMC; ∠NMC=∠MNC ⇒

∠NDF=∠MNC. По признаку равнобедренного треугольника МF=DF.

∆ MDF- равнобедренный.

б)
На ВС отметим середину Р и проведем РF.
PF соединяет середины сторон треугольника, ⇒ PF параллельна АВ и равна АВ:2
PF=ВЕ=10
В четырёхугольнике ВЕFP противоположные стороны взаимно параллельны. ⇒
ВЕFP – параллелограмм
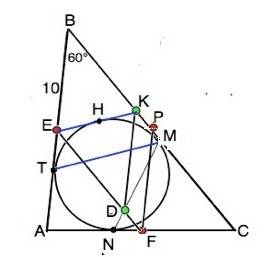
Из т.D проведем DK║PF и получим параллелограмм DKPF., DK=PF=BE

Отметим на АВ точку касания с окружностью буквой Т

Проведем ЕК. Для ∆ ВЕК окружность - вневписанная.

Отметим на ЕК точку Н - точку касания с окружностью.

ЕТ=ЕН, HК=KN, а так как ВТ=ВN, то ЕТ=КN ( расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно полупериметру )=>

ВК=ВЕ=10 (из равных отрезков ВТ и ВN- вычли равные ЕТ и КN)

Но ВК=ЕD. Параллелограмм ВЕDК - ромб.

S (BEDK)=BE²•sin∠EBK=100•√3/2=50√3

S(BED)=S(BEDK):2=25√3 (ед. площади)

4,6(71 оценок)

Ответ:

JollyWolf

17.03.2020

Вариант 1, при АВ>BC.
а) В ∆ АВС отрезок EF - средняя линия, так как соединяет середины
сторон АВ и АС.
ЕF параллельна ВС. Отрезок MD - секущая.
Накрест лежащие углы при пересечении параллельных прямых секущей равны. ∠MDF=∠DMC.
По свойству касательных из одной точки СМ=CN и ∆ МСN - равнобедренный и углы при его основании MN равны (свойство): ∠NMC=∠MNC.
∠MNC=∠FND (вертикальные). Отсюда
∠MDF=∠FND. Треугольник DFN- равнобедренный с основанием DN, FN=FD. Что и требовалось доказать.

б) В любом треугольнике расстояние от вершины треугольника до точки касания вписанной окружности со стороной треугольника, выходящей из данной вершины, есть разность полупериметра треугольника и стороны, противолежащей данной вершине:
То есть CN = (AC + BC+AB)/2 - AB = (AC+BC-AB)/2.
FN=FC-CN = AC/2 - (AC+BC-AB)/2 = AB/2-BC/2.
Но FN = FD (доказано выше) и
ED=EF+FD=EF+FN = BC/2+AB/2-BC/2=AB/2=BE.
Треугольник BED равнобедренный. (ВЕ=ED).
Проведем DK параллельно АВ. Тогда четырехугольник DEBK - ромб и его площадь равна S=BE²*Sin (ABC) = 100*√3/2 =50√3.
Треугольник ВЕD - половина ромба ВЕDK и его площадь равна
Sbed=25√3.

Для второго варианта, при АВ<ВС:
а). EF параллельна ВС, MN - секущая. <NDF=<NMC (соответственные углы). СМ=CN (касательные из одной точки) => треугольник MNC
равнобедренный и <NMC=<MNC (углы при основании). Отсюда <MNC=<NDF и треугольник DFN - равнобедренный с основанием ND.
FN=FD. Что и требовалось доказать.

б). CN = (AC+BC+AB)/2 - AB = (AC+BC-AB)/2.
FN=CN-CF = (AC+BC-AB)/2 - AC/2 - = BC/2-АВ/2.
Но FN = FD (доказано выше) и
ED=EF-FD=EF-FN = BC/2-BC/2+АВ/2=AB/2=BE.
То есть треугольник BED равнобедренный. (ВЕ=ED).
Проведем DK параллельно АВ. Тогда четырехугольник DEBK - ромб и его площадь равна S=BE²*Sin (ABC) = 100*√3/2 =50√3.
Треугольник ВЕD - половина ромба ВЕDK и его площадь равна
Sbed=25√3.

Окружность, вписанная в треугольник abc , касается сторон bc и ac в точках m и n соответственно, e и