что я вам скажу - этими заданиями, в которых есть шаблоны для ответов, куда надо что-то как-то вставить, убивают возможность думать.
Решение простое.
У треугольника есть правило - против большей стороны лежит больший угол, и против меньшей стороны лежит меньший угол.
А теперь собственно решение.
АВ - это меньшая сторона из двух (третью мы вообще не берем в учет), значит против нее лежит меньший угол из двух. А если он тупой, то другой будет еще больше, значит, тоже тупой. Но у треугольника два тупых угла быть не может.
Значит, ответ такой - не может.
<A=67,5°
<D=67,5
<B=112,5°
<C=112,5°
Объяснение:
Дано
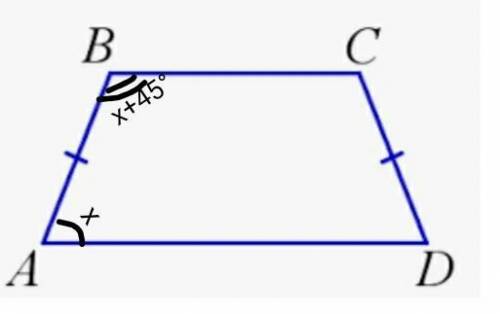
АВСD- равнобокая трапеция
АВ=CD
<A=?
<B=? на 45°больше >А
Найти <А; <В; <С;<D
Сумма углов прилежащих к боковой стороне трапеции равна 180°.
<А+<В=180°.
Пусть градусная мера угла <А будет х°, тогда градусная мера угла <В будет (х+45°).
Составляем уравнение
х+х+45=180
2х=180-45
2х=135
х=135/2
х=67,5° градусная мера угла <А
Градусная мера угла <В (х+45), подставляем значение х
67,5+45=112,5°
По свойствам равнобокой трапеции
<А=<D;
<B=<C
Даны окружность (х-5)²+(у - 5)²=9 и прямая х+у=7.
Точки их пересечения находятся решением системы из заданных уравнений.
Применим подстановки:
Из второго уравнения у = 7 - х подставим в первое.
(х - 5)²+(7 - х - 5)² = 9 или (х - 5)²+(2 - х)² = 9. Раскроем скобки.
х² - 10х + 25 + 4 - 4х + х² = 9. Получаем квадратное уравнение.
2х² - 14х + 20 = 0, сократим на 2: х² - 7х + 10 = 0. D = 49 - 40 = 9.
x1 = (7-3)/2 = 2, x2 = (7+3)/2 = 5.
Находим координаты по у:
у1 = 7 - 2 = 5, у2 = 7 - 5 = 2.
ответ: точки пересечения (2; 5) и (5; 2).