Трапеция равнобедренная, ⇒пары углов, прилежащих к основаниям, равны.
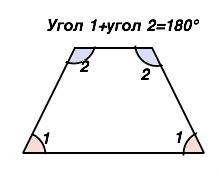
Основания трапеции - параллельны. Боковая сторона - секущая. Поэтому сумма внутренних углов, прилежащих к боковой стороне трапеции, равна 180°. Сумма противоположных углов при разных основаниях равнобедренной трапеции также равна 180°(см. рисунок)
Следовательно, 218° - сумма углов при одном из оснований.
Сумма углов четырёхугольника ( а трапеция - четырехугольник) 360°.
Сумма двух неизвестных углов 360°-218°=142°
Каждый из них равен 142°:2=71° - это ответ.
------------
При пересечении двух прямых образовались вертикальные углы (стороны одного угла являются продолжениями сторон другого угла), это ∡AOD и ∡BOC, ∡BOD и ∡AOC. Вертикальные углы равны => ∡AOD = ∡BOC, ∡BOD = ∡AOC.
Также образовались смежные углы (два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой), это ∡AOD и ∡BOD, ∡BOD и ∡BOC, ∡BOC и ∡AOC, ∡AOC и ∡AOD. Сумма смежных углов равна 180°.
По условию задачи, углы, которые нужно найти, не могут быть вертикальными (по условию углы не равны), значит это пара смежных углов.
Допустим, что ∡AOD на 20° меньше ∡AOC => ∡AOD = ∡AOC – 20°.
∡AOD + ∡AOC = 180°,
∡AOC – 20° + ∡AOC = 180°,
2 × ∡AOC = 200°,
∡AOC = 200° ÷ 2 = 100°;
∡AOD = ∡AOC – 20° = 100° – 20° = 80°
ответ: 100° и 80°