Дата ГЕОМЕТРІЯ
Teme
Контрольна робота N 1. Координати на площині
Користуючись рисунком, визначте координати вершини D прямокутни-
жа ABCD.
UA
D
с (6; 4)
A
В
В
Г
(6:0)
(40)
(0;6)
(0;4)
0 A
B 2
А Б В Г
Укажіть координати середини відрізка NK, якщо м(-3;-2), к(-1;0).
A
Б
В
г
(-2-1)
(-1;-1)
(1; -1)
(1:1)
А Б В Г
Укажіть точку, яка належить четвертій координатній чверті.
Б
B
T
А Б В Г
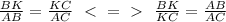
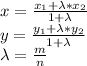
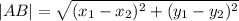
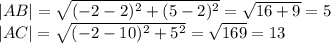
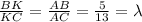
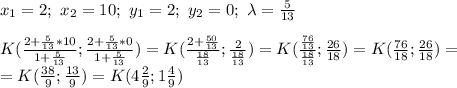
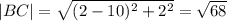
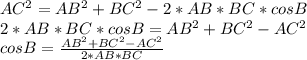
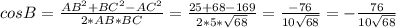
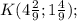 треугольник тупоугольный
треугольник тупоугольный
Допустим, что угол АСМ - это 3х, а угол ВСD ⇒ х.
В сумме углы АСМ и ВСD минус угол МСD дают 180°.
Логично, что если угол BCD - это х, то его половинки - это х/2.
Составим уравнение.
3х+х-х/2=180°
При выполнении несложных математических расчётов получается, что х(угол BCD)=51 3/7°
Следовательно, угол АСВ=180°-51 3/7°=128 4/7°
ответ: 51 3/7° и 128 4/7°.
(это то, что записано в условии. ответы странные, странные и смежные углы... АВС и ВСD не могут быть смежными. смежными могут быть только АСВ и ВСD, как указано в вопросе к задаче... смотри ещё раз условие внимательнее)