відповідь:
пояснення:
проекция вершины s на основание , есть точка пересечения диагоналей квадрата abcd .
положим что это точка h .
l,k середины as, cs соответсвенно , также положим что b1k пересекает bc в точке x , можно теореме менелая , тогда
bb1/b1s * sk/kc * cx/bx=1
или (20-5)/5*(1/1)* (cx/(24+cx))=1 , откуда cx=12 , значит bx=36. аналогично если y точка пересечения lb1 с ab , тогда by=36 .
опустим высоту из точки b1 на основание , основание высоты n будет лежат на диагонали . найдём b1n , подобия треугольников shb и b1nb , тогда sh/b1n = 4/3
по теореме пифагора sh=sqrt(bs^2 - bh^2) = sqrt(bs^2-(bd/2)^2) = sqrt(20^2-(12 sqrt()= sqrt(112) , значит b1n = 3*sqrt(7) и bn=sqrt(15^2-9*7)=9*sqrt(2) . xby равнобедренный и прямоугольный треугольник , положим что m точка пересечения bn и xy , тогда bm=36*sqrt(2) , и mn=bm-bn= 36*sqrt(2)-9*sqrt(2) = 27*sqrt(2) .
тогда если "a" это угол между плослкостью основания и данной плосокостью то
tga=b1n/mn = 3*sqrt(7) / 27*sqrt(2) = sqrt(14)/18 , откуда
a=arctg(sqrt(14)/18) .
S = 18 см2.
Объяснение:
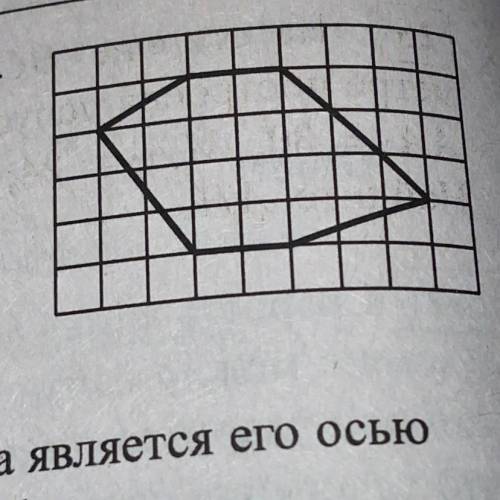
Данную фигуру разделим на 5 сегментов:
1 прямоугольник и 4 треугольника (стороны которых являются диагоналями на отдельно взятых фигурах в данных клетках).
Найдем площади этих фигур:
1). Sпр = 2 * 4 = 8 см2.
2). Sтр1 = 1 * 2 / 2 = 1 см2.
3). Sтр2 = 2 * 3 / 2 = 3 см2.
4). Sтр3 = 3 * 3 / 2 = 4,5 см2.
5). Sтр4 = 1 * 3 / 2 = 1,5 см2.
Суммируя все площади данных фигур вписанных в наш шестиугольник, получим:
6). Sш = 8 + 1 + 3 + 4,5 + 1,5 = 18 см2.