1)
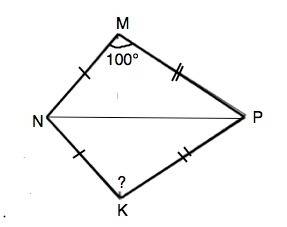
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
2)
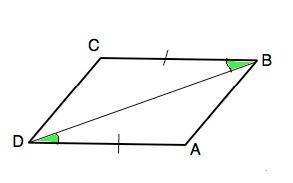
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
8√2см
Объяснение:
Дано:
Треугольник
S=20см² площадь треугольника
b=5см сторона треугольника
<(аb)=45° угол между сторонами а и b
a=? сторона треугольника
S=1/2*a*b*sin<(ab)
sin45°=√2/2
20=1/2*a*5*√2/2
a=20*4/5√2=8√2см