Объяснение:площадь ромба равна произведение диагоналей делённое на 2. Обазначим одну диагональ за х, тогда вторая диагональ х+8. Составляем уравнение.
384=х(х+8)/2
768=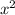 +8
+8
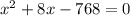
Находим дискриминант. D=64+3072=3136
х1=-8+56/2=24
х2=-8-56/2=-32
значит первая диагональ равна 24 см,а вторая 32 см.
Теперь мы помним что диагонали точкой пересечения делятся пополам. Значит мы имеем треугольник в котором катеты половины от диагоналей, а гипотенуза это сторона ромба. По теореме пифагора:
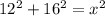
144+256=400
Значит сторона ромба равна: 20 СМ
<BAC=<DEC- это выполнялось бы . если треугольники были бы подобны и тогда CB=AB
Но по условию задачи AB>CB, поэтому <BAC≠<DEC
<DEC=<DCE=<ACB(последние 2 угла вертикальные, поэтому равны)
значит надо доказать что в ΔАВС <A меньше <ACB
по т синусов для треугольника АВС
AB/sin<ACB=CB/sin<A
так как AB>BC и синус угла-возрастает от 0 до 90 градусов, то
следует что делитель первой дроби больше делителя второй
Или sin<ACB больше sin<A-значит <ACB больше <A
и <CDE больше <BAC