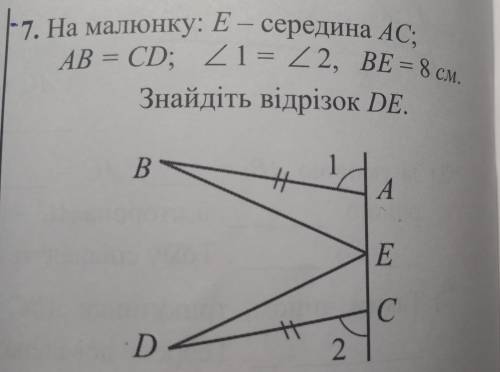
MN=6
Объяснение:
Сумма острых углов прямоугольного треугольника составляет 90°, и сли <В=30°, то <А=90–30=60°. Так как AL биссектриса, то <CAL=<KAL=60÷2=30°. Kаждая. высота, проведённая в каждом треугольнике, образуют другие треугольники, которые являются прямоугольными. В прямоугольном треугольнике катет, лежащий напротив угла В=30°, равен половине гипотенузы, поэтому в ∆ALK LK=½×AL=16÷2=8. Катет KL также является катетом в ∆LKB и гипотенуза ВL в ∆ LKB будет больше в 2 раза больше чем KL, поэтому ВL=8×2=16. Рассмотрим ∆LKB. Если угол В=30°, то угол BLK=60°(90–30=60), а <LKM в ∆LKM=30°, и катет LM=½×KL=½×8=4. Если BL=16, то ВМ=BL–ML=16–4=12. В ∆BMN ВМ - гипотенуза, а MN меньший катет, лежащий напротив угла В=30°, и поэтому равен ½× ВМ, поэтому MN=12÷2=6
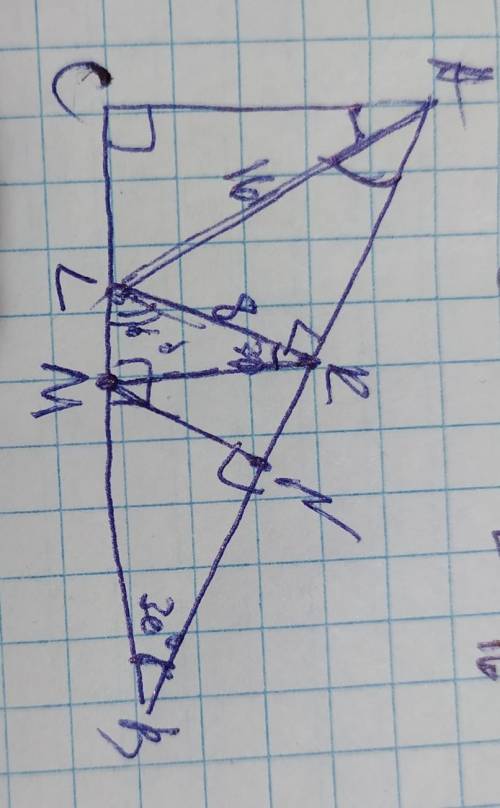
(a + b)/2 = S/(2R);
это - и полусумма оснований, и боковая сторона.
Если теперь опустить перпендикуляр из вершины меньшего основания на большее, то она разобьет основание на отрезки, равные (a - b)/2 и (a + b)/2;
(говоря на правильном математическом жаргоне, проекция боковой стороны равнобедренной трапеции на основание равна (a - b)/2, это легко увидеть, если провести высоты из обеих вершин меньшего основания, между концами высот будет отрезок b, два других равны между собой, то есть (a - b)/2;)
Отсюда (a - b)/2 = √((S/2R)^2 - (2R)^2);
Складывая эти два равенства, легко найти a = S/(2R) + √((S/2R)^2 - (2R)^2);
ну, и b = S/(2R) - √((S/2R)^2 - (2R)^2);