ответ: 198 (ед. площади)
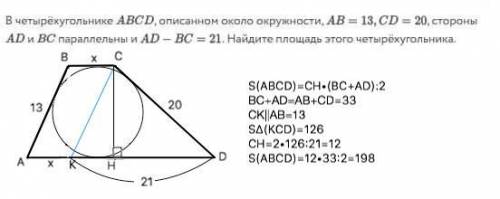
Объяснение: Сделаем рисунок согласно условию.
Так как две стороны четырехугольника АВСD параллельны, это трапеция.
Примем ВС=х. Тогда АD=х+21.
Четырехугольник можно описать около окружности тогда и только тогда, когда суммы его противоположных сторон равны.⇒
ВС+AD=АВ+СD
Площадь трапеции равна произведению высоты на полусумму оснований.
Чтобы найти высоту, проведем СК║АВ. Тогда отрезок АК параллелен и равен ВС=х, КD=21.
По формуле Герона вычислим площадь ∆ КСD, она равна 126 (проверьте).
Высота треугольника и трапеции общая.
СН=2•Ѕ(KCD):KD=2•126:21=12
S(АВСD)=12•(6+6+21):2=198 (ед. площади)
ответ: 54°; 126°; 54°; 126°
В условии не было сказано о рисунке, я не вводил переменных, поэтому претензий к решению не принимаю.
Объяснение: диагонали ромба разбивают его на четыре равных прямоугольных треугольника, т.к. диагонали ромба взаимно перпендикулярны, поэтому, если коэффициент пропорциональности равен х, то 3х+7х+90=180, т.к. сумма углов треугольника равна 180°⇒10х=90; х=9, значит, углы ромба будут соответственно равны 2*3х=6*9°=54° и 2*7х=14°*9=126°; я удвоил углы треугольника, т.к. диагонали являются биссектрисами внутренних углов ромба. а т.к. противоположные углы ромба равны, то искомые углы ромба равны 54°; 126°; 54°; 126°