Нужно опустить перпендикульрную прямую из вершина угла на плоскость. Получится октаэдр
Угол между плоскостью и треугольником это угол между треугол. и треугол. снования.
Кактет треугольника обозначим буквой а. А высоту а корней из 2
Боковая грань октаэдра. Прям. треуг. с уголом в 30 градусов и гипотнузой будет а.Второй же катет будет a/2.
В искомом треуг, образован.высотами известны катет и гипотенуза, по ним определять синус или косинус( на выбор), и потом по ним скать угол.
Синус противолежащий катет к гипотенузе
косинус прилежащий катет к гипотенузе.
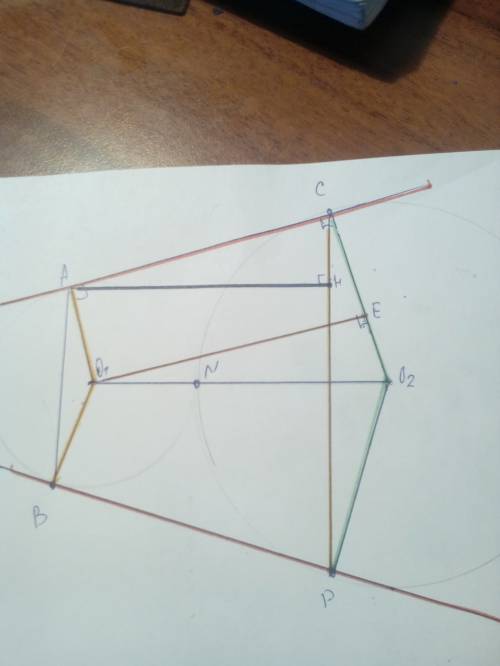
О - центр нижнего основания,
АО перпендикуляр к плоскости нижнего основания, ОН - проекция АН на основание, значит ∠АНО = 45°.
ΔАНО: ∠АОН = 90°, АН = 4√2 см\, ∠АНО = 45°, ⇒ ∠НАО = 45°, ⇒ АО = ОН = х
по теореме Пифагора
x² + x² = (4√2)²
2x² = 32
x² = 16
x = 4 (- 4 не подходит по смыслу задачи)
АО = ОН = 4 см
В треугольнике ОВС ОН - медиана и высота (ОВ = ОС как радиусы),
∠ОВС = ∠ОСВ = (180° - 120°)/2 = 60°/2 = 30°
ΔОВН: ∠ОНВ = 90°, ∠ОВН = 30°, ОН = 4 см, ⇒ ОВ = 8 см
Осевое сечение цилиндра - прямоугольник, одна сторона которого равна диаметру основания, а другая - высоте цилиндра.
S = 2·OB·AO = 2 · 8 · 4 = 64 см²