Объяснение:
У ромба 2 пары равных внутренних углов, сумма которых равна 360°.
Пусть тупой угол равен 2х, тогда острый будет х. Получаем: 2*2х+2х=360
6х=360
х=60.
Значит острый угол ромба равен 60°, а тупой 120°.
Площадь ромба равна половине произведения его диагоналей.
Найдем диагонали.
Известно, что диагонали ромба делят внутренние углы пополами и пересекаются под прямым углом. Исходя из этого, приняв, что диагонали ромба пересекаются в точке О и ∠АВС - тупой, рассмотрим ΔВСО.
Он прямоугольный с ∠ОСВ= 30° и ∠ОВС=60° при гипотенузе ВС. Значит его катет ВО = ВС·sin30° = 3√3,
катет СО=ВС·sin60° = 6√3 · √3 ÷2 = 9
Мы определили длины половин диагоналей ромба.
Тогда площадь ромба АВСD равна
3√3 × 9 × 2 = 54√3 =
1. 120 см²
2. 36√3 см²
3. 270 см²
Объяснение:
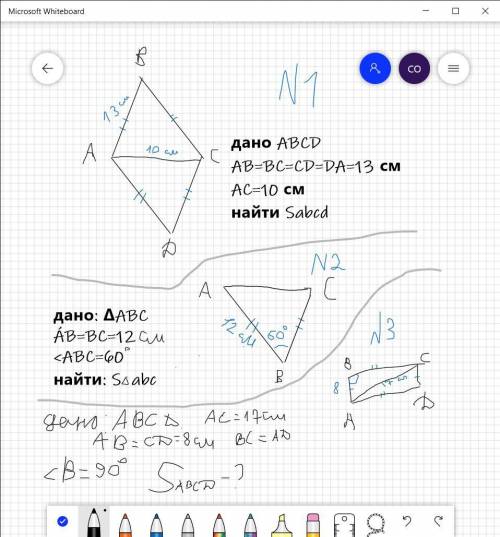
на фото рисунок и дано
1) ΔABC=ΔADC, по трём сторонам => Sabcd=2*SΔabc
По формуле герона
р=(10+13+13):2=36/2=18 см
S²Δabc=p(p-10)(p-13)(p-13)
S²Δabc=18*8*5*5
SΔabc=√(18*8*5*5)=√(9*2*4*2*5*5)=3*2*2*5=60 см²
Sabcd=2*SΔabc=2*60=120 см²
2) Найдем угол при основе (в равнобедренном треугольнике углы при основе равны)
<CAB=<ACB=(180°-<ABC)/2=(180°-60°)/2=120°/2=60°
Если все углы в трегуольнике равны 60°, то это равносторонний треугольник, поэтому все стороны ΔABC равны 12 см
Формула площади равностороннего треугольника: SΔabc=(AB²√3):4=(12²√3):4=(144√3):4=36√3 см²
3) Чтобы найти площадь прямоугольника, андо знать его обе стороны
Рассмотрим прямоугольный треугольник ΔABC. По теореме Пифагора найдем один из его катетов--ВС--,который является и неизвестной стороной прямоугольника
ВС²=АС²-АВ²=17²-8²=(17-8)(17+8)=9*25
ВС=√(9*25)=3*5=15 см
Sabcd=AB*ВС=8*15=270 см²
ответ: 4; 8; 12; 16.
Объяснение:
Т. Фалеса: Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Задачу можно решать разными . Вот один из них.
Пусть точки Е, М, К, Н делят сторону ВС на равные части, и ЕЕ1, ММ1, КК1 и НН1 параллельны АВ ( дано по условию). Тогда СН1=Н1К1=К1М1=М1Е1=Е1А.
По той же теореме Фалеса прямые, проведенные из точек Е1, М1, К1, Н1 параллельно ВС, делят АВ на равные 5 равных частей, каждая из которых равна 20:5=4, и каждый отрезок, проведенный параллельно АВ из Н, К, М, Е, – на равные части.
Тогда НН1 параллельна АВ и равна АВ/5, т.е. НН1=ВТ=4. Остальные отрезки пропорциональны НН1: КК1=2•НН1=2•4=8; ММ1=3•НН1=12; ЕЕ1=4•НН1=16.