1.BOA = DOE по первому признаку, т.к. BO=OD,AO=OE, угол BOA= угол EOD(вертикальные)
2. ABC=BCD по третьему признаку, т.к. AB=BD, AC=CD,BC-общая
3. OMN=QOR по второму признаку, т.к. NO=OQ, угол ONM=угол RQO, угол NOM= угол ROQ
4 DEC = DKC по первому признаку, т.к. DE=DK, DC-общая,угол EDC= угол KDC
5 RQH=RPH по первому признаку,т.к.угол RHQ = угол RHP, QH=HP, RH- общая
6. BAK=BMC. Чертим окружность из точки В, радиус которой равен BK и BM. BK=BM, AB=BC, AK= MC (по третьему признаку)
7. DCE=FEC по первому признаку,т.к. CF=DE, CED=FCE, CE- общая
8. ABD=BCD по второму признаку,т.к. ADB=CBD,ABD=BDC,BD-общая
9.KLN=LMN по третьему признаку,т.к.LK=MN,KN=LM,LN- общая
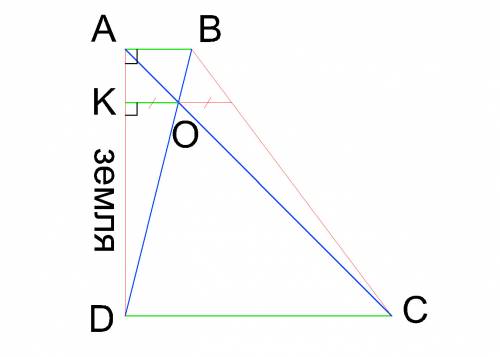
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Объяснение:
a)
∠BAC =180-B-C =180-50-30 =100
∠BAM =∠BAC/2 =50 (AM - биссектриса ∠BAC)
∠BAM=∠B => △BMA - равнобедренный, AM=BM=4 (см)
б)
∠AMC =50+50 =100 (внешний угол △BMA)
△AMD, теорема синусов
AM/sinC =AC/sinAMC => AC =4 sin100/sin30
=8 sin100° =8 cos10° ~7,8785 (см)
в)
△ABC, теорема синусов
AC/sinB =2R => R =8 sin100/2 sin50
=4 sin(2*50)/sin50
=4 2sin50cos50/sin50
=8 cos50° ~5,1423 (см)