Углы каждой пары равны между собой (каквертикальные):
∠1=∠4, ∠2=∠5, ∠3=∠6.
Внешний угол треугольника равен сумме двух внутренних углов, несмежных с ним.
Поэтому ∠1=∠А+∠С, ∠2=∠А+∠В, ∠3=∠В+∠С.
Отсюда сумма внешних углов треугольника, взятых по одному при каждой вершине, равна
∠1+∠2+∠3=∠А+∠С+∠А+∠В+∠В+∠С=2(∠А+∠В+∠С).
Так как сумма углов треугольника равна 180º, то ∠А+∠В+∠С=180º. Значит, ∠1+∠2+∠3=2∙180º=360º.
Когда задают вопрос: «Чему равна сумма внешних углов треугольника?», чаще всего имеют в виду именно сумму углов, взятых по одному при каждой вершине. Поэтому следует уточнить формулировку — нужно найти сумму углов, взятых по одному при каждой вершине или сумму всех внешних углов. Сумма всех шести внешних углов, соответственно, в два раза больше: ∠1+∠2+∠3+∠4+∠5+∠6=2(∠1+∠2+∠3)=720º.
Углы каждой пары равны между собой (каквертикальные):
∠1=∠4, ∠2=∠5, ∠3=∠6.
Внешний угол треугольника равен сумме двух внутренних углов, несмежных с ним.
Поэтому ∠1=∠А+∠С, ∠2=∠А+∠В, ∠3=∠В+∠С.
Отсюда сумма внешних углов треугольника, взятых по одному при каждой вершине, равна
∠1+∠2+∠3=∠А+∠С+∠А+∠В+∠В+∠С=2(∠А+∠В+∠С).
Так как сумма углов треугольника равна 180º, то ∠А+∠В+∠С=180º. Значит, ∠1+∠2+∠3=2∙180º=360º.
Когда задают вопрос: «Чему равна сумма внешних углов треугольника?», чаще всего имеют в виду именно сумму углов, взятых по одному при каждой вершине. Поэтому следует уточнить формулировку — нужно найти сумму углов, взятых по одному при каждой вершине или сумму всех внешних углов. Сумма всех шести внешних углов, соответственно, в два раза больше: ∠1+∠2+∠3+∠4+∠5+∠6=2(∠1+∠2+∠3)=720º.
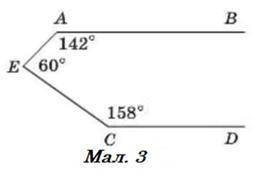
Так, вони паралельні
Объяснение:
Проведемо через точку E пряму EF, яка буде паралельна прямій AB. Отримаємо січну EA, і внутрішній односторонній кут EAB = 142°. Якщо дві паралельні прямі перетинаю третя, то сума внутрішніх односторонніх кутів дорівнює 180°. ∠AEB = 180° - ∠EAB = 180°- 142° = 38°
Пряма EF ділить кут AEC на два кути : ∠AEC i ∠FEC
∠FEC = 60° - ∠AEC = 60° - 38° = 22°
Дві прямі паралельні, якщо сума внутрішніх односторонніх кутів дорівнює 180°. ∠FEC + ∠ECD = 22° + 158° = 180° EF║CD
Оскільки дві прямі, паралельні третій паралельні між собою AB║CD