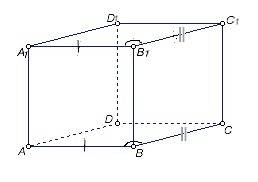
Определение: Параллелепипед — многогранник, у которого шесть граней и каждая из них — параллелограмм.
Требуется доказать, что противоположные грани параллелепипеда параллельны и равны.
Докажем на примере оснований АВСD и A1B1C1D1 данного параллелепипеда.
Отрезки А1В1 и АВ параллельны и равны как стороны параллелограмма АА1В1В, отрезки В1С1 и ВС параллельны и равны как стороны параллелограмма ВСС1В1. ⇒
плоскости оснований параллельны по двум пересекающимся прямым.А1В1 и В1С1 одной плоскости и АВ и ВС противоположной.
Стороны параллелограммов АВСD и A1B1C1D1 равны , соответственные стороны углов А1B1C1 и ABC образованы параллельными прямыми,⇒ углы равны – эти параллелограммы равны, (их можно совместить наложением). Аналогично доказывается параллельность и равенство остальных граней. Доказано.
В объяснении
Объяснение:
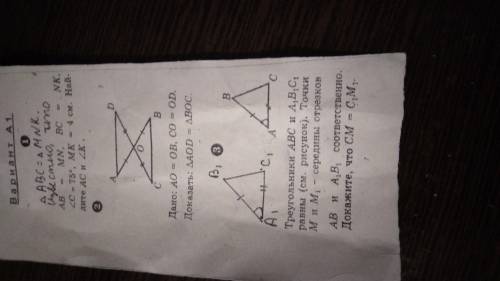
1.Дано: АВС=MNK. AB=MN, BC=NK, угол С=75°, МК=4см
Найти: АС и угол К
Решение:ABC=MNK. Значит, угол С= уголуK=75°, и MK=АС=4см.
2. Дано: АО=ОВ, СО=ОD
Доказать: AOD=BOC
Доказательство: АО=ОВ,СО=ОD значит, AOD=COB-тк углы вертикальны, значит треугольники равны по 1 признаку. (AOD=BOC по 1 приз). ЧТД(что и требовалось доказать)
3. Дано: ABC=A1B1C1, М и М1 - середины отрезков АВ и А1В1
Доказать: CM=C1M1
Доказательство: АВ=А1В1, А1С1=АС. Угол А=углуА1. Проводим линию от M до C, от М1 до С1. А1М1=АМ, АС=А1С1, УГОЛ МАС= УГЛУМ1А1С1. Значит, треугольник МАС равен треугольнику М1А1С1 по 1 признаку(МАС=М1А1С1 по 1 приз) Значит, МС=М1С1. Чтд( что и требовалось доказать)