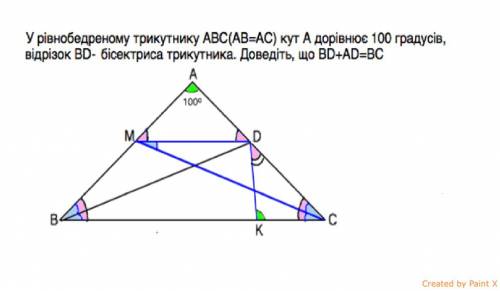
В равнобедренном треугольнике АВС (АВ=АС) угол А равен 100°, отрезок ВD- биссектриса треугольника. Докажите, что ВD+AD=BC ———————
Сделаем рисунок.
∠АВС=∠АСВ=(180°-100°):2=40°
Проведем биссектрису СМ и отрезок МD.
В ∆ АМС и ∆ АDВ стороны АВ=АС по условию.
Угол при А - общий, углы АВD=АСМ =40:2=20° как половины равных углов.
∆ АМС = ∆ АDВ по равной стороне и прилежащим к ней равным углам.
Следовательно, АМ=АD, и ∆ АМD - равнобедренный.
Углы треугольников АВС и АМD при их основаниях равны, они соответственные при пересечении двух прямых секущими, и поэтому МD||ВС (свойство), ⇒
∠ DМС=∠МСВ как накрестлежащие при параллельных прямых и секущей.
А т.к. СМ - биссектриса, то ∠ DСМ=∠ МСD
∆ МDС - равнобедренный, МD=DС.
Отложим на ВС отрезок ВК=ВD Соединим D и К.
∆ КВD - равнобедренный по построению.
Угол КВD=20°. следовательно, углы при КD=по 80°
Тогда угол СКD=100° как смежный углу DKB .
∠ КДС=180°-100°-40°=40° ⇒ ∆ СКD - равнобедренный. и равен треугольнику МАD по стороне и прилежащим к ней углам. КС=АD
ВС=ВК+КС, КС=АD, ⇒ ВD+АD=ВС, что и требовалось доказать.
Задание №1
Объяснение:
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2