Площадь параллелограмма равна 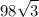 см².
см².
Объяснение:
Требуется найти площадь параллелограмма по известным данным.
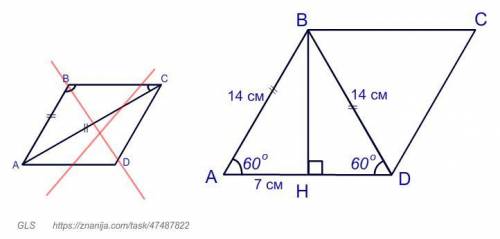
Дано: ABCD параллелограмм, AB = 14 см, диагональ равна стороне, ∠A = 60°.
Найти: S.
Решение.
1) Покажем, что большая диагональ параллелограмма не может быть равна стороне.
В параллелограмме против большего угла лежит большая диагональ.
Сумма углов, прилежащих к одной стороне параллелограмма равна 180° (как односторонние углы при параллельных прямых и секущей).
Тогда один из этих углов острый, а другой - тупой.
Большая диагональ параллелограмма лежит против тупого угла.
Если большая диагональ параллелограмма равна его стороне, то получается равнобедренный треугольник с двумя равными углами при основании, которые являются тупыми. Чего не может быть.
Следовательно, в нашей задаче меньшая диагональ равна стороне параллелограмма.
2) По данным в задаче.
В параллелограмме ABCD ∠A = 60°, диагональ BD равна стороне AB:
BD = AB = 14 см.
ΔABD равнобедренный.
В равнобедренном треугольнике углы при основании равны.
∠ADB = 60°.
Из суммы углов треугольника следует, что ∠ABD = 60°, тогда треугольник равносторонний, сторона AD = 14 см.
(То есть параллелограмм является ромбом).
3) На этом этапе уже можно найти площадь параллелограмма ABCD, но так как просят решить задачу без применения синуса угла (и других тригонометрических функций), найдем ее другим .
Площадь параллелограмма равна произведению основания на высоту.
Найдем высоту параллелограмма.
Проведем в ΔABD высоту BH.
В равнобедренном треугольнике высота является и медианой.
Тогда AH = 14 см : 2 = 7 см.
Из прямоугольногоΔABH (∠AHB = 90°) найдем катет BH.
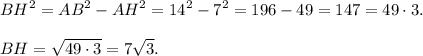
Высота параллелограмма 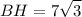 см.
см.
4) Зная высоту BH и основание AD параллелограмма, найдем его площадь.
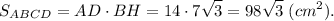
Площадь параллелограмма равна 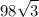 см².
см².
1) Вписанные углы - угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.
2) Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°.
3) Угол с вершиной в центре окружности называется центральным углом.
4) Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
5) 180°
6) Внешние углы - это углы, смежные с углами треугольника.
7) Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
8) S=1/2 a*hª-треугольник. Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
9)