a=6 см
b=8 см
∠C= α = 60°
c-?
1) По теореме косинусов находим третью сторону с:
c² = a² + b² - 2ab·cosα
c² = 6² + 8² - 2 · 6 · 8 · cos60°
c² = 36 + 64 - 2 · 6 · 8 · ¹/₂
c² = 100 - 48
c² = 52
с = 2√13 см
2) Находим площадь треугольника S через две стороны
a и b и углу между ними α по формуле:
ответ: a=6 см
b=8 см
∠C= α = 60°
c-?
1) По теореме косинусов находим третью сторону с:
c² = a² + b² - 2ab·cosα
c² = 6² + 8² - 2 · 6 · 8 · cos60°
c² = 36 + 64 - 2 · 6 · 8 · ¹/₂
c² = 100 - 48
c² = 52
с = 2√13 см
2) Находим площадь треугольника S через две стороны
a и b и углу между ними α по формуле:
ответ: a=6 см
b=8 см
∠C= α = 60°
c-?
1) По теореме косинусов находим третью сторону с:
c² = a² + b² - 2ab·cosα
c² = 6² + 8² - 2 · 6 · 8 · cos60°
c² = 36 + 64 - 2 · 6 · 8 · ¹/₂
c² = 100 - 48
c² = 52
с = 2√13 см
2) Находим площадь треугольника S через две стороны
a и b и углу между ними α по формуле:
ответ: 4*x+10*y-85=0.
Объяснение:
Для того, чтобы все точки прямой a*x+b*y+c=0 находились на равных расстояниях от точек А и В, эта прямая должна быть перпендикулярна прямой АВ и проходить через середину отрезка АВ. Пусть x1 и y1 - координаты точки А, а x2 и y2 - координаты точки В; составим уравнение прямой АВ:
(x-x1)/(x2-x1)=(y-y1)/(y2-y1), (x-4)/(6-4)=(y-4)/(9-4), (x-4)/2=(y-4)/5, y=5/2*x-6. Отсюда следует, что угловой коэффициент этой прямой k1=5/2. А так как прямая a*x+b*y+c=0 перпендикулярна прямой АВ, то её угловой коэффициент k2=-1/k1=-2/5. Пусть точка С - середина отрезка АВ; найдём её координаты x3 и y3:
x3=(x1+x2)/2=5, y3=(y1+y2)/2=13/2. Теперь составляем уравнение прямой a*x+b*y+c=0: y-y3=k2*(x-x3), y-13/2=-2/5*(x-5), 4*x+10*y-85=0.
192. Диагонали параллелограмма пересекаются и точкой пересечения О делятся пополам. Треугольники АВС и АДС равновеликие (равны по площади); треугольники АОД и СОД тоже равновеликие; треугольники АОК и КОД тоже равновеликие. Следовательно, если SАДС=1/2отSАВСД, то SАОД=SСОД=1/4отSАВСД. А SКОД=1/8отSАВСД. В сумме SСОД и SКОД=3/8отSАВСД. То есть отношение 3:8.
193. Большая сторона - гипотенуза (5х). Катеты соответственно равны 4х и 3х. Треугольники, образованные высотой, прямоугольные. Все три подобны между собой. Составим пропорцию на основе подобия треугольников: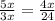
; 
; 
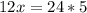. Если х=10, то гипотенуза =10*5=50, катеты: 10*4=40, 10*3=30. Периметр P=50+40+30=120.