
Объяснение:
Решение.
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два.
S = 15 √3 / 2
ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
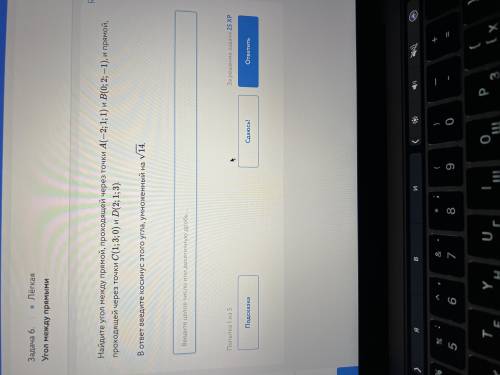
Угол между двумя прямыми равен углу между их направляющими векторами. Координаты направляющих векторов ( из координат конца вычтем координаты начала) АВ(2 ;1 ;-2), СD(1 ; -2 ; 3) . Косинус угла равен частному от деления скалярного произведения на длины направляющих векторов.
АВ*СD=2-2+6=6,
|AB|=√(4+1+4) =3,
|CD|=√(1+4+9) =√14.
cos( AB, CD) =6:(3*√14) =2/√14
ответ 2