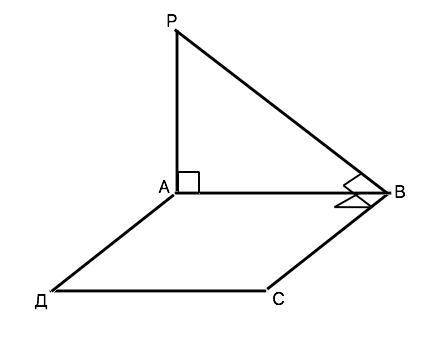
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
Можно. Медиана прямоугольного треугольника к гипотенузе равна её половине и делит исходный на два равнобедренных.
Так как углы равнобедренных треугольников равны, проще всего делить равнобедренный прямоугольный треугольник. Сумма его острых углов 90°, и каждый равен 45° ( см. рис. 1).
Другой случай - медиана, проведенная из прямого угла, делит исходный на остроугольный и тупоугольный с вершиной на гипотенузе. . Тупоугольный треугольник можно разделить на 3 равнобедренных, два крайних при этом будут между собой равны. (см. рис.2). Равные углы окрашены в одинаковые цвета. Доказать, что эти треугольники равнобедренные, наверняка сможете без труда.

ответ: so = 8.
Объяснение:
Розглянемо трикутник acb, він рівнобедрений ac =bc ( в основі правильної чотирикутної піраміди лежить квадрат) кут b =90 градусів ( в квадрата всі кути по 90 градусів). Отже трикутник abc прямокутний і рівнобедрений. За теоремою Піфагора знайдемо ac. ac2 = ab2 + bc2. ac = 16 корені квадратний з 2.
Розглянемо трикутник asc - він рівнобедрений отже so - висота, медіана і бісектриса. ao = oc. кут o = 90 градусів. ao = 1/2 ac. ao = 8 корені квадратний з 2.
Розглянемо трикутник aos - він прямокутній. За теоремою Піфагора as2 = ao2+so2 звідси виходить що so2 =as2 - ao2. so = 8.