ответ: 67°
Объяснение:
посмотрим на угол В с двух сторон
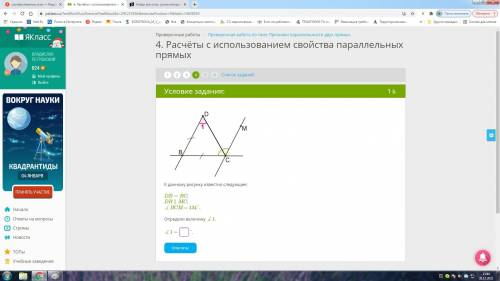
1) т.к. DB+BC, то по свойству углов при основании равнобедренного треугольника ∠1=∠BCD, тогда ∠В=180°-2*∠1,
2) т.к. DB║MC при секущей ВC, то ∠DBC+∠ВСM=180°как сумма внутренних односторонних, тогда ∠В=180°-∠ВСM=180°-134°=46°
сопоставляем 1) и 2), получаем, 180°-2*∠1=46°⇒∠1=(180°-46°)/2=134°/2=67°
-короче, т.к. ∠1=∠DCB, и ∠1=DСМ, как внутренние накрест лежащие при DB║MC и секущей DC, то ∠1=∠DCB=∠DСМ=134°/2=67°
Рисунок - во вложении.
Т.к. E и F - внутренние точки отрезка АВ, и по условию АЕ=BF, то
для EB=AB-AE и для AF=AB-BF следует, что EB=AF.
Рассмотрим прямоугольные ΔADF и ΔВСЕ. У них: 1) АD=BC (противолежащие стороны прямоугольника); 2) AF=EB (по доказанному выше). Значит, ΔADF = ΔВСЕ по двум катетам.
Из равенства этих треугольников следует, что ∠DFA=∠СЕВ. Отсюда, ΔEGF - равнобедренный с основанием EF, тогда GF=GE. Доказан пункт Б).
Т.к. АВСD - прямоугольник, то АВ║CD. Тогда ∠EFG=∠GDC(как накрестлежащие при секущей FD) и ∠FEG=∠GCD (как накрестлежащие при секущей ЕС). Отсюда, ΔDGС - равнобедренный с основанием DC, тогда DG=GC. Доказан пункт A).

67 градусов
Объяснение:
Судя по рисунку, BCD=DCМ=0.5ВСМ=67°
BCD - равнобедренный треугольник, углы при его основании равны, тогда BDC=BCD=67°
Или другим путем с тем же ответом, угол С, смежный углу ВСМ равен 180-134=46°, соответствующий ему DBC при параллельных прямых тоже равен 46°, а углы при основании в треугольнике тогда равны (180-46)/2=67°