18,75 ед. изм.
Объяснение:
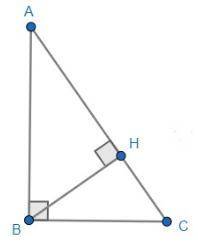
Дано: ΔАВС, ∠В=90°, ВН - высота, АН=20, ВН=15. ВС - ?
ΔАВН - прямоугольный, по теореме Пифагора
АВ=√(АН²+ВН²)=√(400+225)=√625=25.
ВН²=АН*СН; 15²=20*СН; 20*СН=225; СН=11,25.
АС=20+11,25=31,25
По теореме Пифагора
ВС=√(АС²-АВ²)=√(976,5625-625)=√351,5625=18,75.
Для начала найдём все углы: <A - <B/2; <B = <C-30.
Объявим угол <A — как переменную "x", угол B объявим как: 2x, угол C объявим как: 2x+30.
<A = x
<B = 2x
<C = 2x+30
x+2x+2x+30 = 180°
5x+30 = 180°
5x = 150° ⇒ x = 150/5 = 30° ⇒ <A = 30°
<B = 30*2 = 60°
<C = <B+30 = 90°.
Как мы видим, наш треугольник ABC — прямоугольный, так как имеет один прямой угол(<C).
AB — гипотенуза, известный нам катет — BC.
Катет BC — лежит напротив угла A(30°).
Теорема 30-градусного угла в прямоугольном треугольнике такова: катет, протолежащий углу 30-и градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2; BC = 2 ⇒ AB = 2*2 = 4.
Вывод: AB = 4.
Даны вершины треугольника: А(1;-3;4), В(2;-2;5), C(3;1;3).
Находим векторы и их модули.
АВ = (1; 1; 1), |AB| = √(1² + 1² + 1²) = √3.
BC = (1; 3; -2), |AB| = √(1² + 3² + (-2)²) = √14.
АC = (2; 4; -1), |AB| = √(2² + 4² + (-1)²) = √21.
Косинусы углов находим по формуле:
cos A = (b² + c² - a²)/(2bc).
Вот результаты расчёта:
Треугольник АВС
a(ВС) b(АС) c(АВ) p 2p S
3,741657387 4,582575695 1,732050808 5,028141945 10,05628389 3,082207001
14 21 3
1,286484558 0,44556625 3,296091137 1,889365914 9,5 3,082207001
cos A = 0,629941 cos B = -0,308607 cos С = 0,933139
Аrad = 0,889319 Brad = 1,884524 Сrad = 0,367749
Аgr = 50,954246 Bgr = 107,975284 Сgr = 21,07047.
18,75 см
Объяснение:
Пусть СН=х см, тогда ВН²=20*х; 225=20х; х=11,25; СН=11,25 см.
АС=20+11,25=31,25 см.
АВ=√(ВН²+АН²)=√(225+400)=√625=25 см.
ВС=√(АС²-АВ²)=√(976,5625-625)=√3515625=18,75 см.