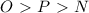- всё это конечно углы.
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
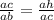
теперь подставим наши значения в эту пропорцию:
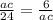
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см
2. Рассмотрим треугольник DBE.
Это равнобедренный треугольник, так как по условию BD = BE.
∠BDE = ∠BED, так как это углы при основании равнобедренного треугольника.
3. Определим ∠BDA и ∠BEC.
∠BDA и ∠BDE смежные, поэтому
∠BDA = 180° - ∠BDE.
Аналогично ∠BEC и ∠BED смежные, поэтому
∠BEC = 180° - ∠BED.
Так как ∠BDE = ∠BED, то и ∠BDA = ∠BEC.
4. Рассмотрим треугольники ABD и CBE.
Эти треугольники равны по двум сторонам и углу между ними:
BD = BE и AD = CE - по условию;
∠BDA = ∠BEC.
Следовательно, и стороны BA и BC равны.
Значит, треугольник ABC -равнобедренный.
Знаешь ответ?