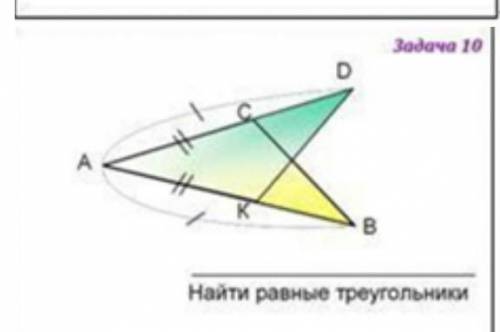
Задача: Основой прямой призмы является равнобедренный треугольник ABC, в котором АС=ВС, АВ = 6 см, ∠BAC = α, причем tgα=3/4. Найти объем призмы, если площадь ее боковой поверхности в два раза больше за площадь ее основания.
Формула объема прямой призмы:
V = S₀·h,
где S — площадь основы,
h — высота призмы
Высоту можно найти, использовав формулу боковой площади призмы:
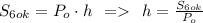 ,
,
где Po — периметр основы призмы.
Необходимо найти периметр и площадь ΔABC (основа призмы).
Рассмотрим ΔABC:
Проведем высоту CH на основу AB. Получим два прямых треугольника.
Р-м ∠ACH:
AH = AB/2 = 6/2 = 3 (см)
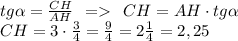
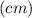
Гипотенуза AC за т. Пифагора равна:
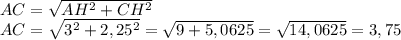
Найдем периметр ΔABC:
P = AC·2+AB = 3,75·2+6 = 7,5+6 = 13,5 (см)
Найдем площадь ΔABC:
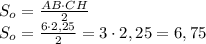
Найдем высоту призмы:
По условию, площадь боковой поверхности призмы в два раза больше площади ее основания:
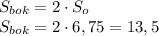
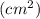
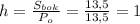
Наконец, найдем объем данной призмы:
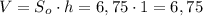
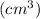
ответ: Объем призмы равен 6,75 см³.
Объяснение:
ё1)Дан треугольник ABC A(6;0), B(6;8) и C(3;4).
Определи AB = ; BC = ; AC =
Треугольник ABC
равнобедренный ? разносторонний ? равносторонний?
Решение.
АВ=√(6-6)²+(8-0)²=√(0+64)=8
ВС=√(3-6)²+(4-8)²=√(9+16)=√25=5
АС=√(3-6)²+(4-0)²=√(9+16)=√25=5. Две стороны равны ,значит треугольник равнобедренный .
2)ABCD-прямоугольник,A(16;3), B(20;7), C(18;9) и D(14;5). Найти S.
Решение. ABCD-будет прямоугольником если противоположные стороны равны +диагонали равны.
АВ=√(20-16)²+(7-3)²=√(16+16)=4√2,
ВС=√(4+4)=2√2,
СD=√(16+16)=4√2,
DА=√(4+4)=2√2, Т.о. АВ=СD , ВС=DА и Оп четырехугольник превращается в параллелограмм.
АС=√(4+36)=2√10,
ВD=√(36+4)=2√10.И Оп параллелограмм. превращается в прямоугольник.