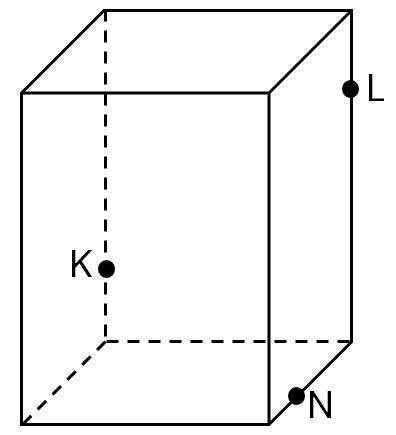
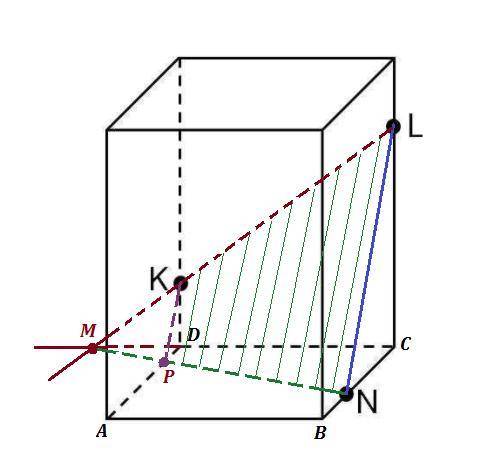
Так как точки N и L лежат в одной плоскости, то их можно соединить .
Так как точки L и K лежат в одной плоскости, то их тоже можно
соединить . Но продлим прямую LK до пересечения с ребром CD в
точке М .
Соединим точки М и N . Прямая MN пересечёт AD в точке Р .
Точки Р и К лежат в одной плоскости , соединяем их .
Получим сечение NLKP .
Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Осноположником геометрии можно считать Евклида. В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». В развитии Геометрия можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.
Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Геометрия, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.Геоме́трия (от др. ... γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.
если их можно совместить и при наложении они совпадают.
Если при наложении они совпадают. Равные отрезки имеют одинаковые длины.
Если при наложении они совпадают. т.е. вершины совпадут. а лучи, выходящие из вершин, тоже при наложении совпадают. Равные углы имеют равные градусные меры.
Треугольники называют равными, если при наложении друг на друга они совпадают. У равных треугольников все три стороны одного равны трем сторонам другого. То же можно сказать и об углах.
2 представьте, построили два равных прямоугольных треугольника, у которых катеты по 3 см 4 см, а гипотенузы по 5 см. у меня нет возможности попасть в приложение. поэтому не могу Вам кинуть рисунок. Но это не сложно. АВ=ТР= 3 см, ВС= РК=4см, АС=ТК=5 см, и тогда треугольники АВС и ТРК равны.
3.
1.FDE
2.KNM
3.SKT
DBC
5. MKC
см фото
Объяснение:
1. соединяем т K, L и N
2. Поскольку грани на которых находятся точки L (левая грань) и К, N (правая грань) ║
Из точки К проводим отрезок КЕ ║LN получаем т. Е
3. соединяем т. Е до т. N