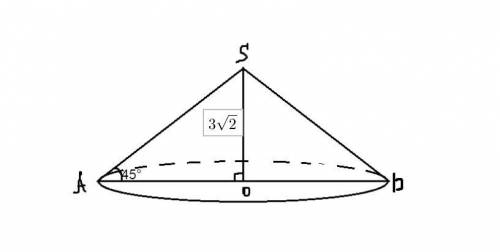
Найдите площадь боковой поверхностью конуса у которого высота равна 3 корня из двух см и составляет с образующей угол 45 гр.
Рассмотрим треугольник SOA. Это прямоугольный треугольник. Так как угол SAO по условию равен 45 градусам ⇒ треугольник равнобедренный ⇒ Радиус основания ОА = 3√2 (см.)
Тогда по т. Пифагора найдем образующую конуса SA:
SA² = (3√2)² + (3√2)²
SA² = 18 + 18
SA² = 36
SA = 6 (см.)
Площадь боковой поверхности конуса находим по следующей формуле:
S(бок.) = п * r * l , где r - радиус основания, l - образующая.
S(бок.) = 6 * 3√2 *п = 18√2п (см²)
ответ: 18√2п (см²)
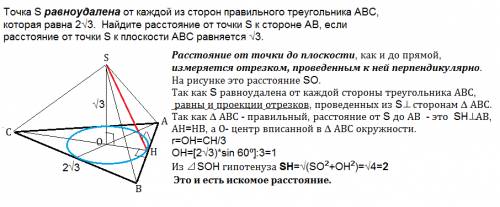
Точка S равноудалена от каждой из сторон правильного треугольника ABC, которая равна 2√3. Найдите расстояние от точки S к стороне AB, если расстояние от точки S к площади ABC равняется √3.
-------------------
Расстояние от точки до плоскости, как и до прямой, измеряется отрезком, проведенным к ней перпендикулярно.
На рисунке это расстояние SO.
Так как S равноудалена от каждой стороны треугольника АВС, равны и проекции отрезков, проведенных из S перпендикулярно сторонам ∆ АВС.
∆ АВС - правильный, расстояние от S до АВ - это SH⊥АВ, АН=НВ, а О- центр вписанной в ∆ АВС окружности.
r=OH=CH/3
OH=[2√3)*sin 60º]:3=1
Из ⊿ SOH гипотенуза SH=√(SO²+OH²)=√4=2
64π м²
Объяснение:
AB=r=6м радиус меньшего шара.
АС=R=10м радиус большего шара.
∆АВС- прямоугольный треугольник
По теореме Пифагора
ВС=√(АС²-АВ²)=√(10²-6²)=8м.
BC- радиус сечения, площадь которого необходимо найти.
Sсеч=π*ВС²=8²π=64π м²