1. Равные многоугольники имеют равные площади (аксиома площадей).
Отсюда —
Равные четырёхугольники равновелики (равные по площади).
2. Обратное утверждение : "Если у четырёхугольников равные площади, то они равны".
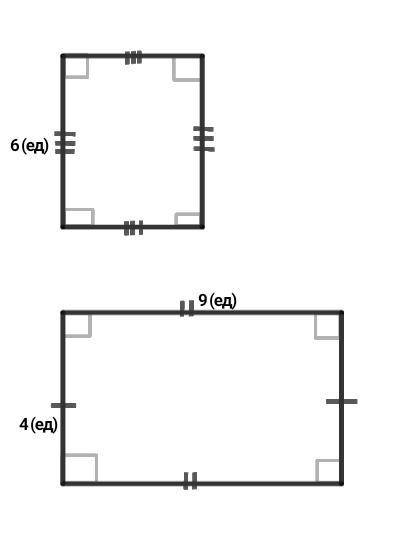
Рассмотрим квадрат со стороной 6 (ед) и прямоугольник с смежными сторонами, равными 9 (ед) и 4 (ед).
Логично, что эти фигуры не могут быть равными между собой, ведь у равных четырёхугольников равны все соответствующие элементы (у квадрата все стороны равны по 6 (ед), а у прямоугольника стороны попарно равны по 9 (ед) и 4 (ед), тоесть они никак не могут быть равными).
Однако же —
Площадь квадрата = квадрат стороны = (6 (ед))² = 36 (ед²).
Площадь прямоугольника = произведение смежных сторон = 9 (ед)*4 (ед) = 36 (ед²).
Мы доказали, что квадрат и прямоугольник не равны, однако имеют равные площади.
Поэтому обратное утверждение не всегда верно (верно только тогда, когда четырёхугольник равны).
Отрезки большей боковой стороны a=50 и b=8. Отрезки касательных, проведенных из одной точки, равны. Проведем диаметр вписанной окружности, соединив точки касания на основаниях - отсеченные отрезки оснований равны a и b. Опустим высоту из вершины меньшего основания - отсеченный отрезок основания равен a-b. По теореме Пифагора высота равна
h= √((a+b)^2-(a-b)^2) =2√(ab)
Боковая сторона, перпендикулярная основаниям, равна высоте (расстояние между параллельными постоянно). Суммы противоположных сторон описанного четырехугольника равны, периметр равен
P= 2(2√(ab)+(a+b)) =2(√a+√b)^2
P= 2(√50+√8)^2 =2(7√2)^2 =196