1) В основании правильной пирамиды МАВС лежит правильный треугольник, все стороны основания равны АВ=Р:3=18√3:3=6√3 см. Апофема МН=5 см, высота МО=4 см. а) S(бок)=половина произведения апофемы на периметр основания. S(бок)=5•18√3•1/2= 45√3 см²
б) S(ABC)=a²√3/4=(6√3)²•√3/4=27√3 см². в) S(полн)=45√3+27√3=72√3 см²
V(MABC)=S(АВС)•h/3=27√3•4:3=36√3 см Вершина высоты правильной пирамиды проецируется в центр основания ( точку пересечения медиан, которая делит их в отношении 2:1, считая от вершины угла). Апофема правильной пирамиды, её высота и треть высоты основания образуют прямоугольный треугольник МОН. По т.Пифагора НО=√(MH²-MO²)=√(4-1)=√3 см. Тогда СН=3•ОН=3√3 см. Все углы правильного треугольника равны 60°, поэтому ВС=АВ=СН:sin60°=3√3:(√3/2)=6 см. S(бок)=3•МН•АВ:2=3•2•6:2=²см если обязательно в решении нужно использовать данный по условию объем. V=S(ABC)•h:3 ⇒ S=3V:h. S=a²√3/4 ⇒ a²=4S:√3=(12V:h):√3=12•3√3:√3=36. a=√36=6 см S(бок)=3•МН•АВ:2=3•2•6:2=18 см²
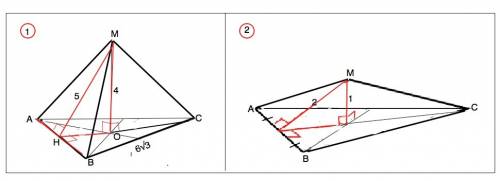
4) Для нахождения площадей S1,S2,S3 надо найти высоты тр-ков.
Из тр-ка АOS- прям.: LSAO=45, тогда тр-к равноб.
и SO=AO=4, AS=4*корень из 2 ( !длина бокового ребра пирамиды).
Из тр-ка СВS- равноб.: SH- высота,
тогда SH = корень из ((4*корень из2)^2-2^2 )=корень из 28=2*корень из7.
Из тр-ка АСS- равноб.: SH1- высота,
тогда SH 1= корень из ((4*корень из2)^2-(2*корень из 3^2 ))=
= корень из 20=2*корень из 5.
5) Таким образом
S бок = 0,5*8*4+0,5*4* 2*корень из 7 + 0,5*4 *корень из 3* 2*корень из 5=
= 16+ 4* корень из 7 + 4* корень из 15 (кв.ед).
Теряю квалификацию ( слишком длинно)....:(((
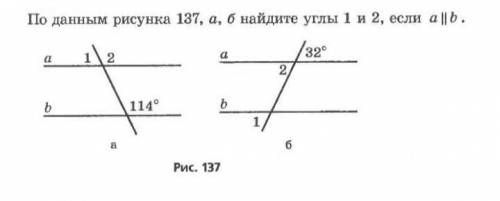
а)∠1=66°
б)∠2=32°,∠1=32°
Объяснение:
а) угол, равный 114° и ∠3 - называются соответственными углами при параллельных прямых а и b и секущей.
Соответственные углы равны, то есть ∠3=114°
∠1 и ∠3 - смежные углы. Их сумма равна 180°, ⇒∠1=180°-114°=66°
б) угол равный 32° и ∠2 - вертикальные углы.
Вертикальные углы равны ⇒∠2=32°
∠1 и ∠2 - соответственные углы. Соответственные углы равны.
⇒ ∠1 = 32°
2 вариант:
∠1 и угол в 32° являются внешними накрест лежащими углами.
Внешние накрест лежащие углы равны: ∠1=32°
∠1 и ∠2 - соответственные углы. Соответственные углы равны.
⇒ ∠2 = 32°