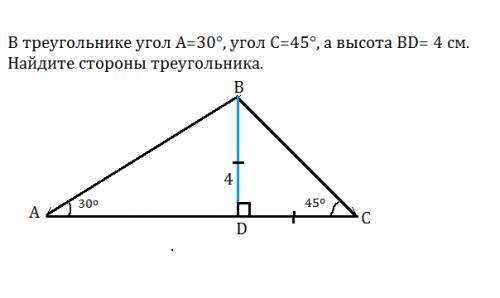
В треугольнике угол A=30° угол C=45° а высота BD= 4 см.
Найдите стороны треугольника.
----------------------
Высота ВД противолежит углу, равному 30º. ⇒ BD равна половине гипотенузы ∆ АВД.
Гипотенуза АВ=4*2=8 см.
АD найдем по т.Пифагора:
АD²=АВ²-ВD²
АD=√(64-16)=√48
АD=4√3 см
В прямоугольном ∆ ВDС острый угол ВСD=45º, ⇒ угол СВD=45º,
∆ СВD - равнобедренный, СD=ВD=4 см
По т.Пифагора ВС=4√2 см ( проверьте)
Тогда АС=АD+DС=4√3+4=4(√3+1)
Стороны равны
АВ=8,
ВС=4√2
AC =4(√3+1)
-----------
Если Вы уже изучали тригонометрические функции, то можно использовать их значение для заданных углов.
АВ=ВD:sin30º=4:0,5=8 см
BC=BD:sin45º=4:(√2)/2=4√2 см
АС=АD+DС=4√3+4=4(√3+1) см
МА и ВС - скрещивающиеся прямые, т.к. не лежат в одной плоскости и не пересекаются.
Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямымПроведем прямую НK параллельно прямой AМ.
Прямая НK перпендикулярна плоскости АВС (так как она параллельна AB). По т. о параллельных прямых в пространстве: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к этой плоскости.
И если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой лежащей в этой плоскости. КН перпендикулярна прямой ВС, лежащей в этой плоскости. КН║МА ⇒ МА⊥ВС, ч.т.д.