1. От точки А строим угол, равный данному (описано в первом
варианте) и на полученной второй его стороне откладываем отрезок
АВ, равный данной гипотенузе. Из точки В опускаем перпендикуляр на
прямую "а". Для этого:
Из точки В проводим окружность любого радиуса R, чтобы пересекла
прямую "а" в точках G и Q. Из точек G и Q тем же радиусом проводим
две дуги, пересекающиеся в точке M. Прямая ВМ - искомый перпендикуляр.
На пересечении прямых ВМ и "а" ставим точку С.
Соединяем точки А,В и С и получаем прямоугольный треугольник АВС
с прямым углом <C и с заданными гипотенузой и острым углом.
2. На прямой "а" откладываем отрезок, равный одной из сторон, например, АС. Проводим окружности с центрами в точках А и С радиусами, равными двум другим сторонам, например, АВ и СВ соответственно. В точке пересечения этих окружностей получаем точку В. Треугольник построен.
3. На прямой "а" откладываем отрезок, равный стороне АВ, к которой проведена высота СН. Проводим окружность радиуса ВС с центром в точке В. Из точки В к прямой "а" восстанавливаем перпендикуляр и на нем откладываем отрезок ВР, равный высоте СН. Из точки Р проводим перпендикуляр к отрезку ВР и в точке пересечения этого перпендикуляра с проведенной ранее окружностью ставим точку С.
Соединив точки А,С и В получаем искомый треугольник.
P.S. Построение перпендикуляра к прямой в заданную точку не описываю - это стандартное построение.
Если радиус равен 2 √3 тогда длина хорды, стянутой дугой в 60 градусов будет равна радиусу так как образуется равносторонний треугольник если соединить края хорды с центром окружности в основании конуса. Если высота конуса равна 4√3 то высота треугольника , образованного в разрезе будет определяться по теореме Пифагора из треугольника образованного высотой конуса, высотой треугольника полученного в разрезе и высотой равностороннего треугольника полученного в результате соединения краев хорды с центром основания. Высота треугольника лежащего в основании конуса будет равна 3
Следовательно по теореме Пифагора высота разреза будет равна √(9+48)
Теперь чтоб узнать площадь разреза нужно найти площадь треугольника полученного в разрезе , а это произведение высоты √57 на основание 2 √3 и делим пополам. Получаем площадь разреза 3√19
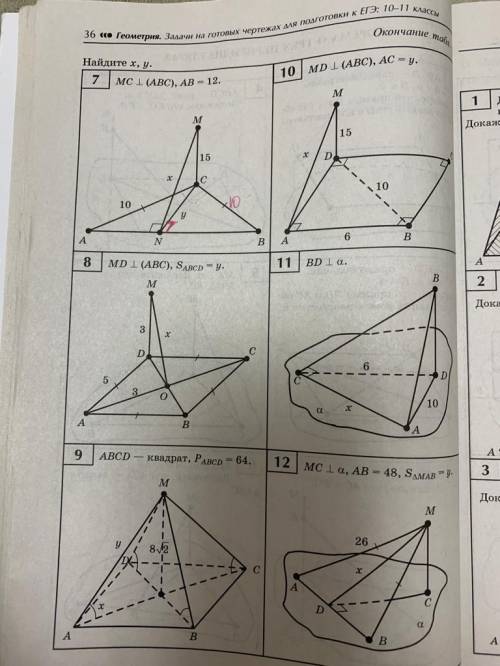
MD⊥(АВС) , AB=BC=CD=AD , AD=5,AO=3,MD=3. Найти площадь ABCD , расстояние от точки М до точки О
Объяснение:
1) Все стороны АВСD равны , значит это ромб . Диагонали ромба взаимно-перпендикулярно⇒ ∠АОВ=90°.
ΔАОВ- прямоугольный , по т Пифагора ,
ОВ=√(АВ²-АО²)=√(5²-3²)=4 (ед).
2) Диагонали ромба точкой пересечения делятся пополам , поэтому ВD=8 ед , АС=6 см.
S( ромба )=1/2*d₁*d₂ , S( ромба )=1/2*8*6=24 (ед²).
3) Тк МD⊥ (ABC) , то MD⊥DO .
ΔMDО прямоугольный , по т Пифагора ,
МО=√(MD²+DО²)=√(3²+4²)=5 (ед).