
Высоты тупоугольного треугольника, проведенные из вершин острых углов, пересекают прямые, содержащие их стороны, вне треугольника.
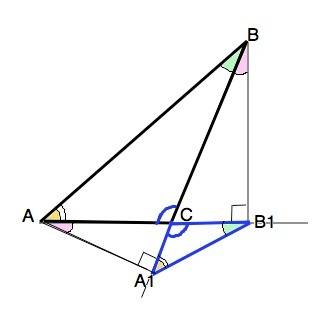
Рассмотрим прямоугольные ∆ АСА1 и ∆ ВСВ1.
Острые углы при С у них равны как вертикальные.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны. ⇒
∆ АСА1 ~ ∆ ВСВ1
Тогда синусы их равных углов равны, т.е. отношение сходственных катетов к гипотенузам, равно. СА1/ АС=СВ1/ВС
III признак подобия треугольников.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Доказано.
№1
По свойству углов в треугольнике, их сумма должна быть равна 180. Т.е. ∠В=180-45-90=45 следовательно, ∠В=∠А=45, треугольник равнобедренный, поэтому боковые стороны (катеты) равны. По т. Пифагора:
Нам известны все стороны, теперь нужно найти S и Р
№2
а - катет = 1. ∠В=60. Опять же по с-ву углов в треугольнике, ∠А=30, а по с-ву угла в 30* с=2а=2
По т. Пифагора
Нам известны все стороны, теперь нужно найти S и Р
№3
Опять же, по свойству угла 30*,
По т. Пифагора:
Нам известны все стороны, теперь нужно найти S и Р
№4
a=b, следовательно, это равнобедренный прямоугольный треугольник. По т. Пифагора:
Периметр и площадь по известной формуле.
№5
По т. Пифагора:
Периметр и площадь по известной формуле.