S полной поверхности параллелепипеда = 2 S основания + 4 S боковой грани
S основания = S ромба =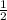
* на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
это равносторонний треугольник
2 диагональ из равностороннего треугольника со стороной a, и высотой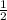 a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами 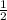*a (половина 1 диагонали), гипотенуза = a.
По т.пифагора: (корень из 3)*a/2
2 диагональ (равна корень из 3)*a
площадь основания = (корень из 3)*a*a/2.
найдем высоту. 45 град. угол между диагональю параллелепипеда и 2 диагональю ромба.
в треугольнике, образованном диагональю параллелепипеда диагональю ромба и боковой стороной параллелепипед один угол 45 град, второй = 90 град, то третий будет 180 - 45 - 90.
данный треугольник - равносторонний и высота равна диагонали ромба т.е. (корень из 3)*a. (в следствии)
Следовательно площадь боковой грани = a*(корень из 3)*a
Итого П.П.П. = 2*(корень из 3)*a*a/2 + 4*a*(корень из 3)*a = 5*(корень из 3)*(a в квадрате) (формулой)
Опустим из вершины тетраэдра D высоту DН на АС.
∆ АDН - прямоугольный, угол АDН=90°-45°=45°⇒
АН=DН=АD•sin45°=6
СН=АС-АН=14-6=8
По т. Пифагора DС=√(DH²+СH²)=√(36+64)=10 см
∆ADB=∆ADC по двум сторонам и углу между ними⇒ BD=CD и
∆ BDC равнобедренный, высота DM является его медианой, ⇒ ВМ=СМ=16:2=8 см
DM делит ∆ BDC на два равных "египетских" треугольника с отношением сторон DM:BM:BD=3:4:5. ⇒DM=6 (см).
S ∆ BDC=DM•BC:2=6•16:2=48 см²