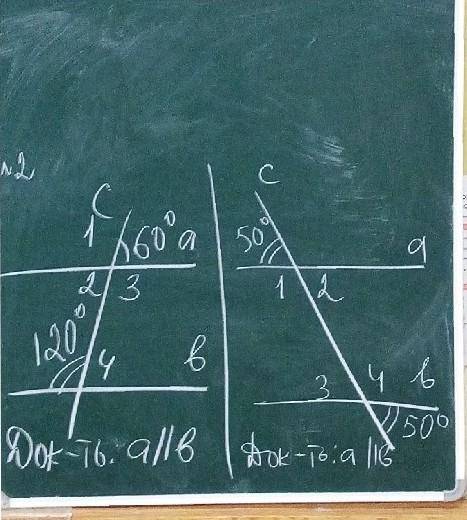
Номер 1
<60=<2=60 градусов,как вертикальные
<2+<120=60+120=180 градусов-это односторонние углы
Если при пересечении двух прямых а и b секущей c односторонние углы в сумме равны 180 градусов,то прямые параллельны
ИЛИ
<3+<60=180 градусов,как смежные
<3=180-60=120 градусов
<3=<120 градусов,как накрест лежащие,при а || b и секущей с
Если при пересечении двух прямых секущей накрест лежащие углы равны между собой,то прямые параллельны
Углы 50 градусов являются накрест лежащими,если при пересечении двух прямых секущей накрест лежащие углы равны между собой,то прямые параллельны
а || b при секущей с
Объяснение:
Отрезок МС перпендикулярен CD, поскольку CD перпендикулярно всей плоскости МBC (Это потому, что МВ перпендикулярно всем прямым в плоскости АВСD, а ВС перпендикулярно CD) так что в ПРЯМОУГОЛЬНОМ треугольнике МВС МС - гипотенуза, а катеты 13 и 10.
МС = корень(269);
через прямую МВ проводим ПЛОСКОСТЬ, перпендикулярную АС, точку пересечения с АС обозначим К. МК и ВК перпендикулярны АС (объяснение - в предыдущем предложении).
ВК - высота к гипотенузе прямоугольного треугольника со сторонами 5 и 10.
Длина гипотенузы АС^2 = (5^2 + 10^2) = 5*корень(5);
BK*AC = AB*BC = 50; ВК = 2*корень(5);
Из прямоугольного треугольника МВК с катетами ВК и МВ находим МК
МК = корень(169 + 20) = корень(189) = 3*корень(21);
Так противоположные углы параллелограмма равны (разность противоположных углов =0), то разность двух смежных углов равна 70 градусов.
Пусть дан параллелограмм ABCD и
угол A-угол В=70 градусов (1)
По свойству смежных углов параллелограмма (их сумма равна 180 градусов)
угол А+угол В=180 градусов (2)
Сложив равенства (1) и (2), получим
2*угол А=70 градусов +180 градусов
2*угол А=250 градусов
угол А=250 градусов:2;
угол А=125 градусов
угол В=угол А-70 градусов=125 градусов -70 градусов=55 градусов
ответ: 55 градусов, 125 градусов
1) в первом случае, внешние накрест лежащие углы равны, внутренние накрест лежащие углы тоже равны , допустим это угол Х и он равен 60°, и внутренний угол (120°) и этот угол Х в сумме равны 180°, значит прямые параллельны
Объяснение:
2) во втором случае, внешние накрест лежащие углы равны, поэтому они параллельны.
т.е если равны внешние накрест лежащие углы, то обязательно будут равны и внутренние накрест лежащие углы. И для этого случая теорема доказана. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны