полное условие - прикрепленное вложение.
Задание 1.
На картинке отмечены односторонние углы при прямых a и b и секущей с, в сумме они должны давать 180°.
110°+70°=180° ⇒ 180°=180° ⇒ a || b
Задание 2.
На картинке отмечены односторонние углы при прямых a и b и секущей с, в сумме они должны давать 180°.
125°+65°=180° ⇒ 190°=180° ⇒ a и b не параллельны
Задание 3.
На картинке отмечены накрест лежащие углы при прямых a и b и секущей с, они должны быть равны.
40°=40° ⇒ a || b
Задание 4.
На картинке отмечены односторонние углы при прямых a и b и секущей с, в сумме они должны давать 180°.
180°-a+a=180° ⇒ 180°=180° ⇒ a || b

Объяснение:
1) S=a+b/2*h=8+6/2*5=35(cm²)
2) Маючи сторону і одну діагональ знайдемо іншу діагональ і потім знайдемо площу ромба. Діагоналі пересікаються під прямим кутом, тому легко знайдемо половинку діагоналі , а потім і цілу діагональ.Назвемо її ВД і вона =16 см , S ромба через діагоналі буде:АС*ВД/2=12*16/2=96 см²
3)S=а+в/2*h 2S=(a+b)*h a+b=2S/h=2*40/4=20 cm
4)Маємо прямокутню трапецію, маємо периметр, маємо площу, а також маємо меншу бічну сторону, яка також буде висотою прямокутньої трапеції, нам треба знайти іншу бічну сторону трапеції.
Знайдемо суму основ трапеції (а+в) S=а+в/2*h а+в=2S/h=2*27/3=18 см.
Тепер знайдемо невідому бічну сторону трапеції: Р-периметр=26 см
26-(3+18)=5 см. Друга бічна сторона трапеції =5 см
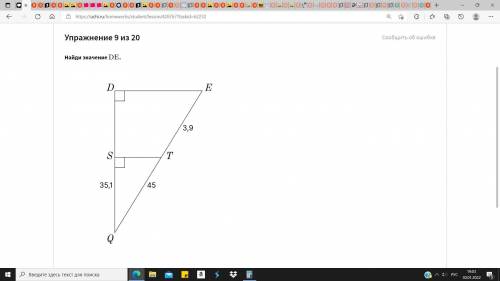
≈30,644 ед.
Объяснение:
ΔQDE подобен ΔQST по двум углам;
QE=45+3,9=48,9 ед.
По теореме Пифагора
ST=√(QT²-QS²)=√(2025-1232,01)=√792,99≈28,2 ед.
Из подобия треугольников следует: QE/DE=QT/ST
DE=QE*ST:QT=48,9*28,2:45≈30,64 ед.