
Картинка в этой задаче действительно желательна.
Объем правильной треугольной призмы равен произведению площади основания на высоту призмы.
Площадь основания - это площадь правильного треугольника со стороной а.
Формула площади равностороннего треугольника
S=(a²√3):4
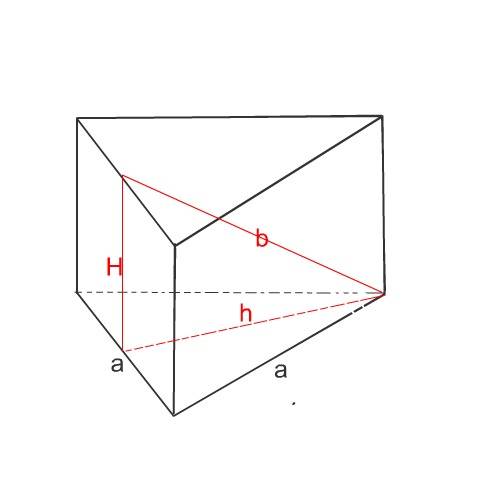
Высоту призмы найдем из прямоугольного треугольника,
катеты в котором- высота призмы и высота треугольника=основания,
а гипотенуза - данное в условии расстояние b от вершины одного основания до противолежащей стороны другого основания.
Высота правильного треугольника находится по формуле
h=а√3):2
Высоту призмы найдем по теореме Пифагора:
Н= √(b²-h²)=√(b²-3а²:4)
V= (a²√3):4)·√(b²-3а²:4)
Так, теперь рассмотрим треугольник ABC (который основной) и ABH например( если что, то AH это высота. нарисуй треуг. что бы потом не запутаться)
прямоугольный треуг. с проведенный к гипотенузе высотой делится на 3 подобных треугольника.( там по 2 углам получается)
поэтому наш ABC подобен треуг. ABH.
Еще раз повторю, нарисуй трег. чтобы видеть, что чему подобно.
Найдем коэффициент подобия
AB тут выступает в роли гипотенузы треугольник ABH, надеюсь это понятно.
теперь остается найти высоту
как-то так