1) подобны ли треугольники АВС и МРК,если АВ=10 дм,АС=20дм,ВС=15 дм,МР=10 см,МК=15см,а РК=20 см?
2) основание высоты прямогульного треугольника,опущенной гипотенузу делит её на отрезки 9 и 16. найти катеты треугольника и его площадь.
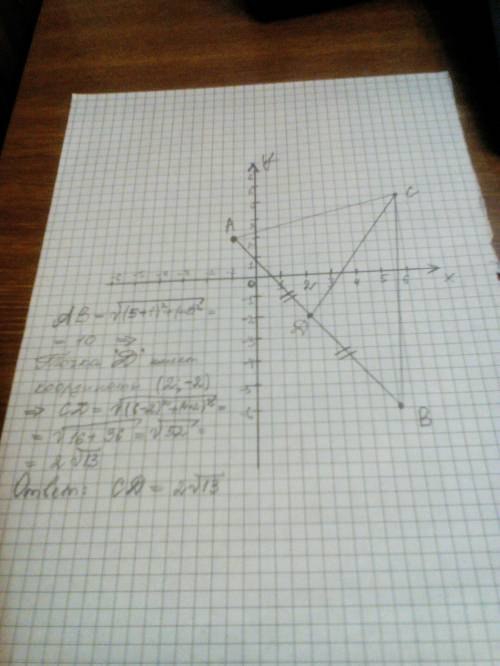
3) отрезки АВ и ДС лежат на параллельных прямых,а отрезки АС и ВД пересекаются в точке М. найдите МС,если АВ=14, ДС=56, АС=40.
р = (6+7+5)/2 = 9
S = √(9(9-6)(9-7)(9-5)) = √216 = 14.69693846
r = S / p = 14.69693846 / 9 = 1.63299316.
Так как треугольники подобны, то площади пропорциональны квадрату коэффициента пропорциональности.
Найдем высоту треугольника АВС:
Hb= 2S / b = 2*14.69693846 / 7 = 4.1991253.
Высота треугольника ВКМ меньше на 2 радиуса:
hb = Hb - 2r = 4.1991253 - 2*1.63299316 = 0.93313895
Коэффициент пропорциональности к = hb / Hb = 0.9331389 / 4.1991253 = 0.22222222,
к² = 0.04938272.
Тогда S(BKM) = 14.69693846* 0.04938272 = 0.725774739 кв.ед.
А периметр равен Р(АВС)*к = (6+7+5)*0.22222222 =
= 18*0.22222222 = 4.
2) В этой задаче не улавливается зависимость между заданными площадями треугольников.
3) В этой задаче что то неверно в условии.
Если диаметр , проходящий через вершину В, делит хорду KL пополам, то эта хорда перпендикулярна диаметру. При этом она не пересекает сторону ВС - смотри прилагаемый чертёж.