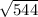
Каждая сторона треугольника меньше суммы двух других сторон.
Рассмотрим несколько случаев.
Случай 1. Боковые стороны равны 3 см.
Итак, все стороны должны удовлетворять неравенствам.
3 см+3 см > 7 см ⇒ 6 см > 7 см - это уже неверно, поэтому боковая сторона не может быть 3 см.
Случай 2. Боковые стороны равны 7 см.
7 см+7 см > 3 см ⇒ 14 см > 3 см
7 см+3 см > 7 см ⇒ 10 см > 7 см
7 см+3 см > 7 см ⇒ 10 см > 7 см.
Итак, все стороны удовлетворяют неравенствам. Треугольник со сторонами 7 см, 7 см, 3 см.
Периметр треугольника = 7 см+7 см+3 см = 17 см.
ответ: 17 см.
Точки A,B,C,D
все выглядит так
точки B,C,D образуют треугольник ,который является основанием трехгранной пирамиды ABCD
где т.А -вершина пирамиды
у пирамиды три боковых грани-треугольники ABC,ACD,ABD
у каждого треугольника основание ВС,CD,BD -соответственно
у каждого треугольника средняя линия KM,MP,KP -соответственно
каждая средняя линия параллельная своему основанию и плоскости (BCD)
три средних линии пересекаются и образуют единственную плоскость (КМР),которая параллельна плоскости (BCD)
ДОКАЗАНО
Площадь S = 9*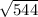
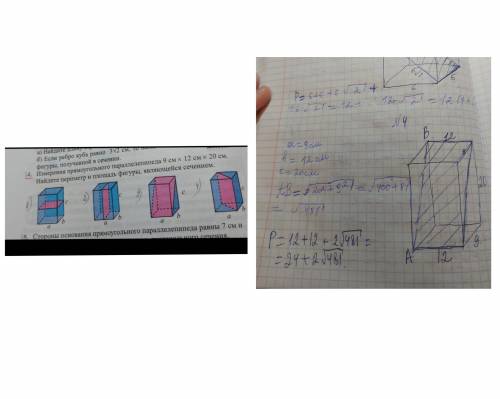
Периметр P = 18 + 2*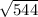
Объяснение:
Сечением является параллелограмм, т. к. две противоположные стороны равны и параллельны.
Диагональ боковой грани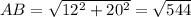
Периметр параллелограмма P = 2(a + AB) = 2(9 +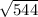
) = 18 + 2*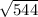
Площадь параллелограмма S = a * AB (в общем случае площадь параллелограмма равна высота*основание; у нас основание AB, и a ⊥ AB по т. о 3-х перпендикулярах, т. е. a - высота)
S = 9*