1) Через две различнье точки всегда можно провести окружность.
ДА
2) Через две различные точки всегда можно провести окружность , и притом только одну.
НЕТ, окружностей бесконечно много.
3) Через две различные точки всегда можно провести окружность данного радиуса.
НЕТ, если расстояние меж точками больше диаметра окружности - то её не построить
4) Через две различные точки всегда можно провести окружность радиуса, paвного между этими точками , и притом только одну.
Ошибка в вопросе!
Если расстояние меж точками = диаметру окружности - то да, её можно построить только одну.
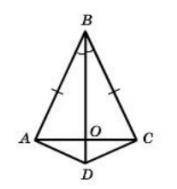
Дано: АВ = ВС. ∟ABO = ∟CBO.
Довести: ∟DAO = ∟DCO.
Доведення:
Розглянемо ∆ABD i ∆CBD.
За умовою АВ = ВС, ∟ABO = ∟CBO, BD - спільна сторона.
За I ознакою piвності трикутників маємо: ∆ABD = ∆CBD.
Звідси маємо: AD = DC.
Отже, ∆ADC - рівнобедрений (АС - основа).
За властивістю кутів рівнобедреного трикутника маємо: ∟DAO = ∟DCO.
Доведено.